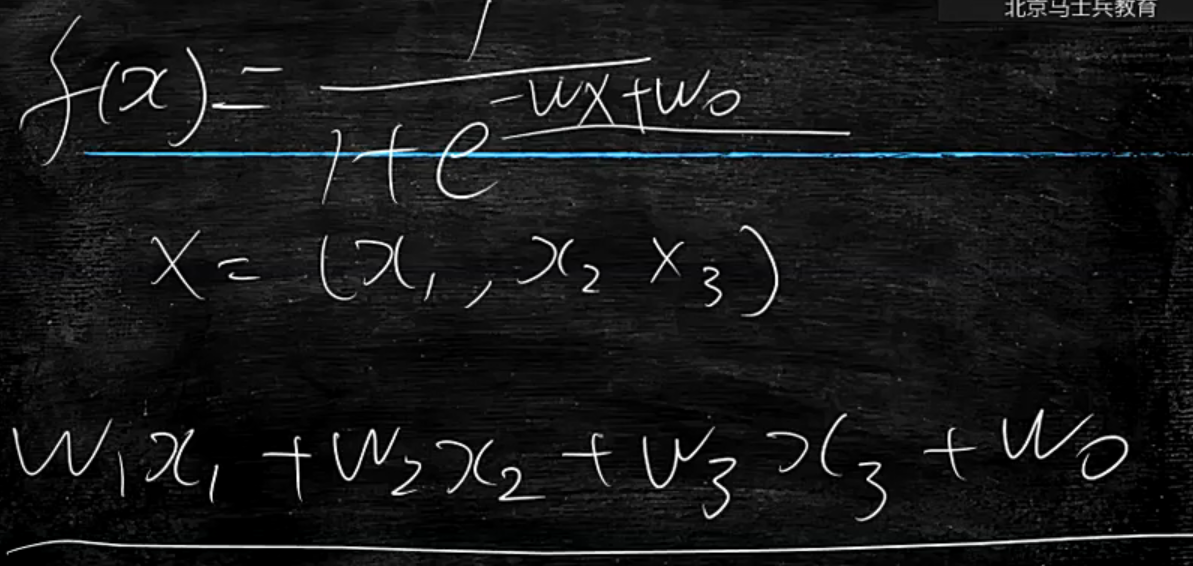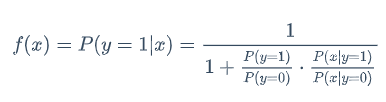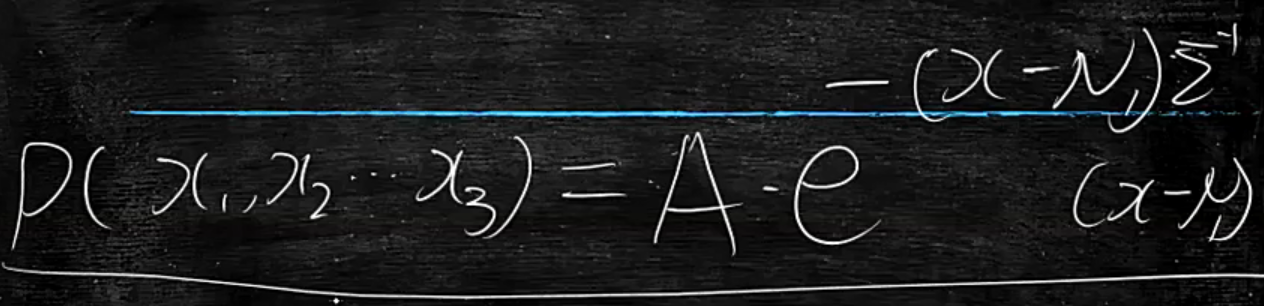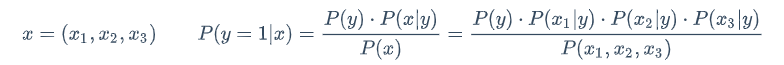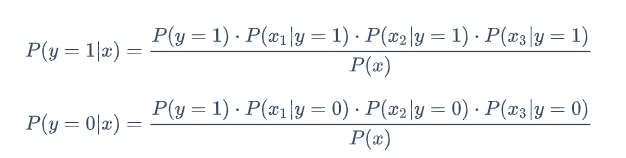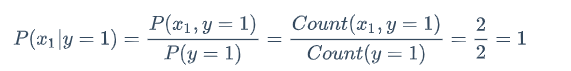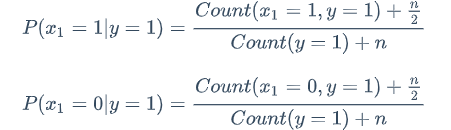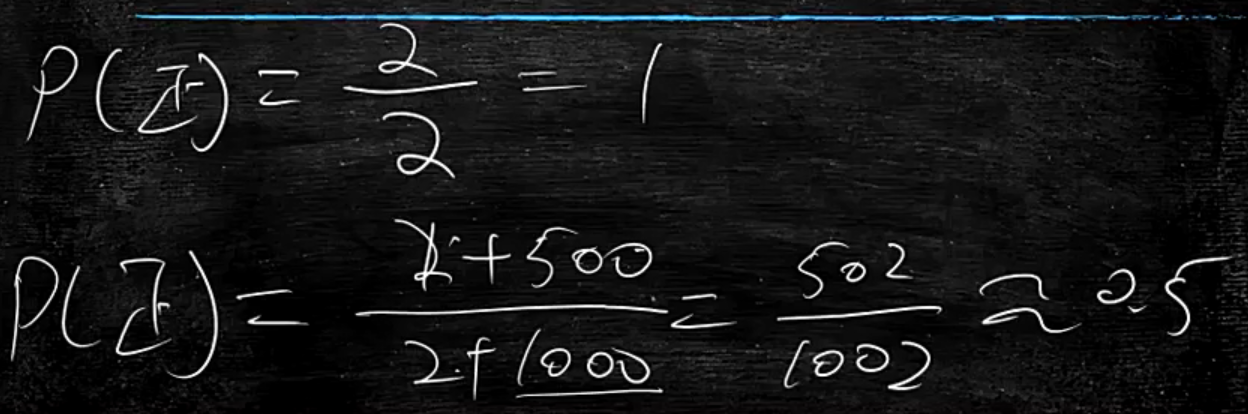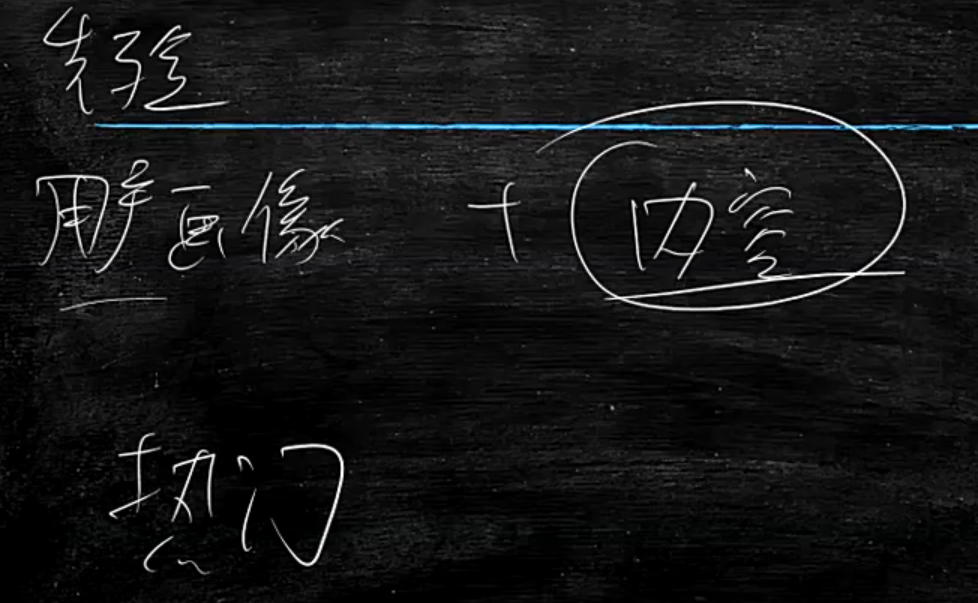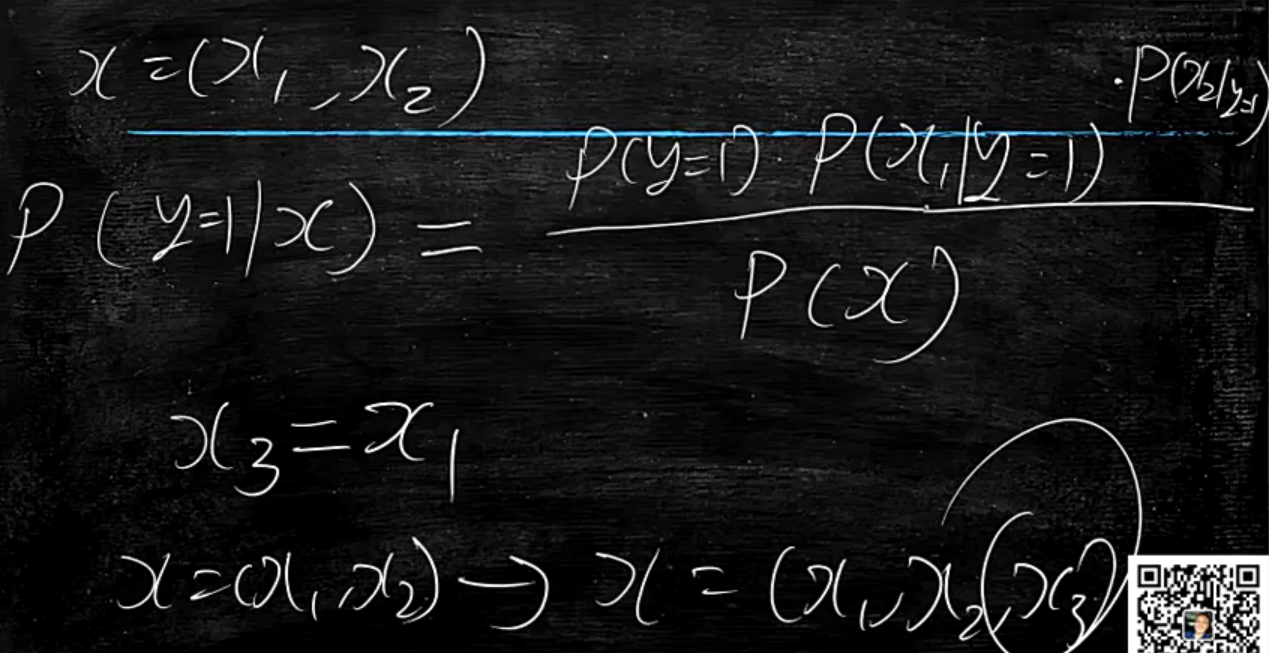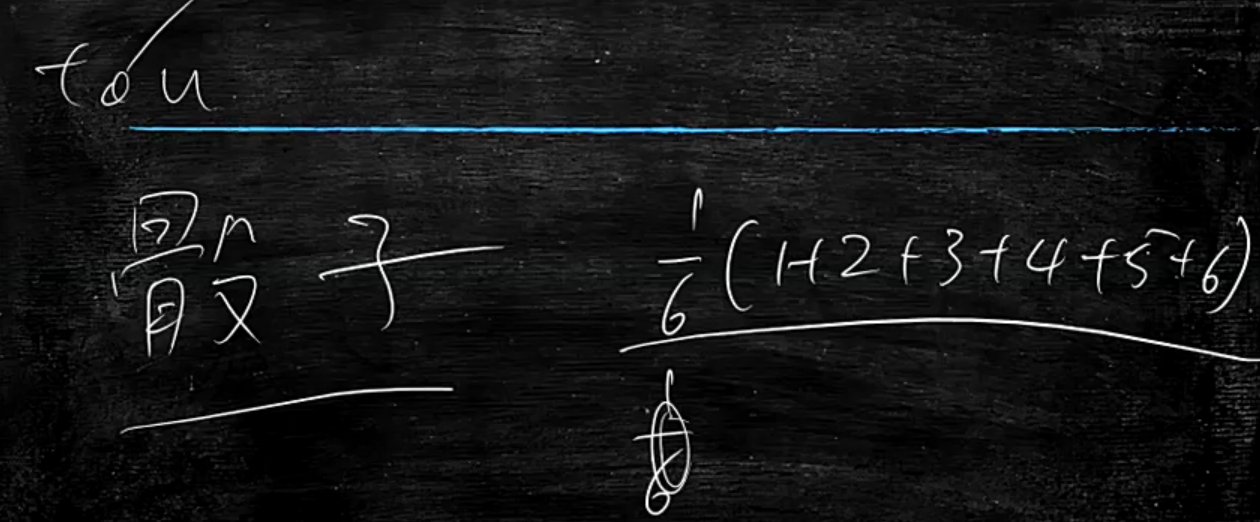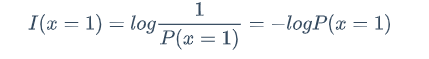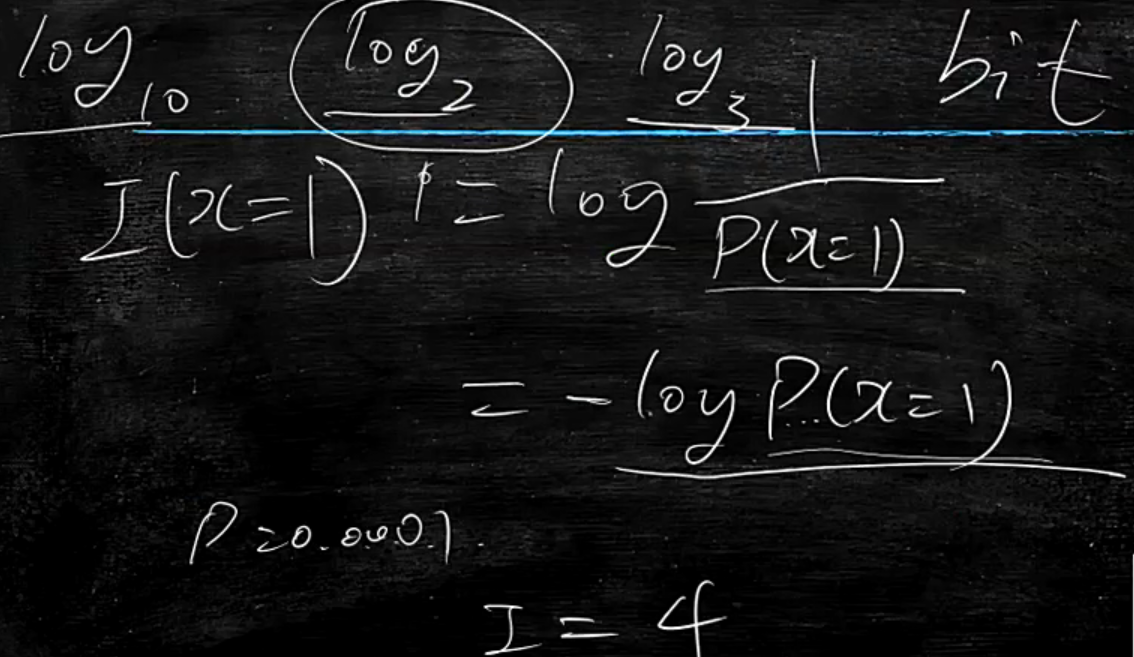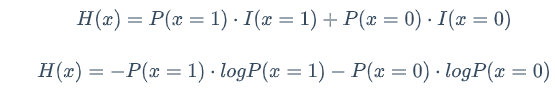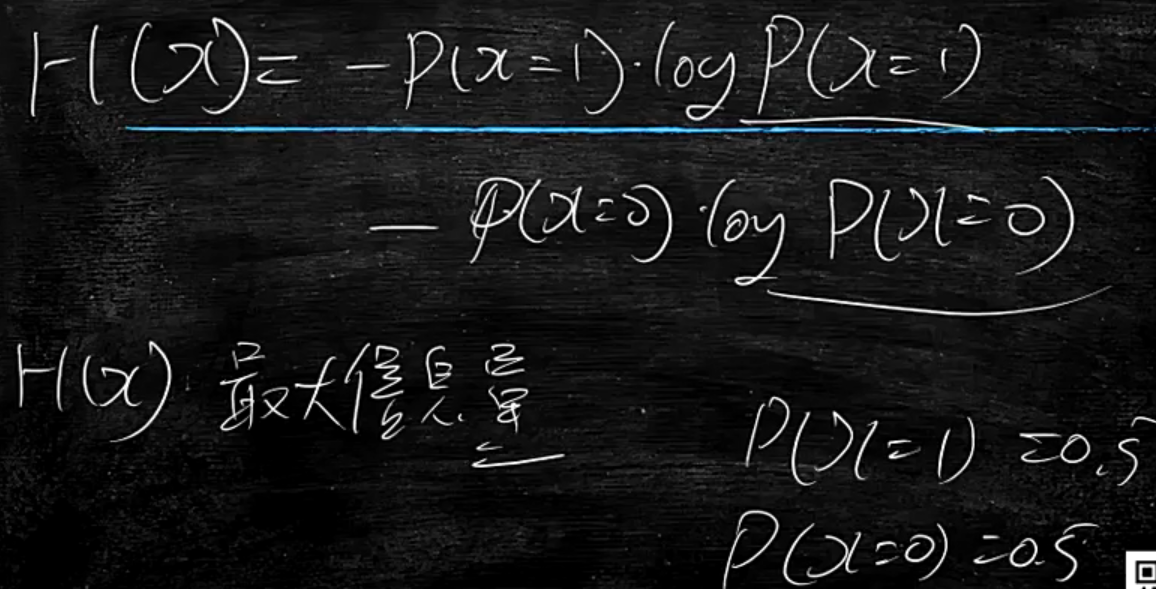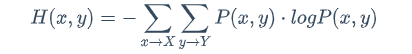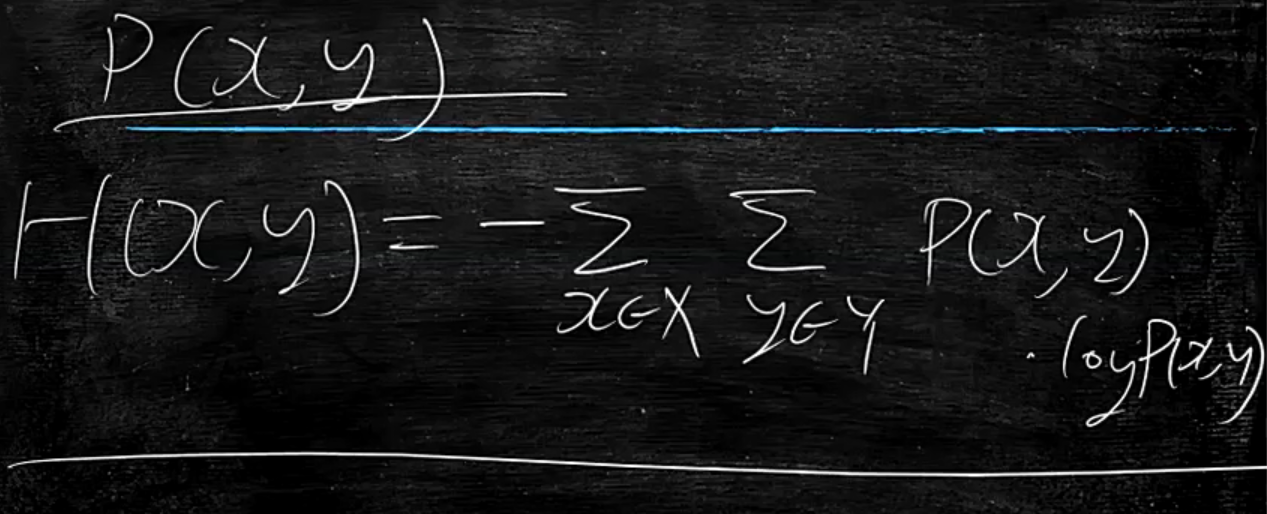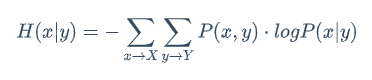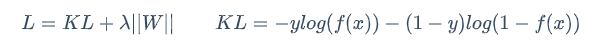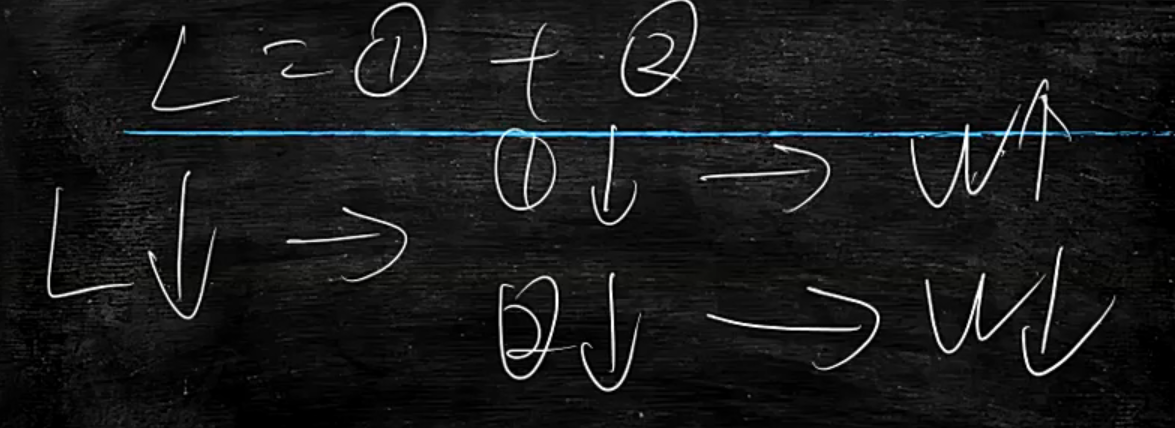# 朴素贝叶斯模型：简单背后蕴含的有效

回顾一下

基于逻辑回归的传统机器学习与深度学习(主线)

所以之前讲解逻辑回归时非常的细，因为很重要，作为深度学习的基础

深度学习理解为是个大脑，逻辑回归理解为神经元

所以在逻辑回归主要研究神经元的构造，在深度学习则研究神经元之间的一种联系

w1x1+w2x2+w3x3+w0这个式子有何缺点？

比如中X(x1,x2,x3)是相亲市场评测数据，用来判别人在相亲市场的受欢迎程度

x1=身高，x2=体重，x3=收入这里需要很多的数据，难免会有一项数据缺失，实际场景中数据不全的问题

比如：x2这一项根本不知道数据是什么，那么逻辑回归是不是就没办法使用了？那么有什么解决方案吗？

这就要探究逻辑回归最大的问题是耦合，即f(x1,x2,x3)不能把这些x单独拆出来，如下图，耦合在一起了

所以说目的是解耦

那么就要探究一下，逻辑回归耦合的根本原因是什么？

答：高斯分布即正态分布

分类最终是要求解这个概率P(y=1|x)

根据贝叶斯公式：

最终代数运算得出：

前面讲解到P(x|y=1)与P(x|y=0)是个正态分布

多元正态分布

根本原因：可以看出，是多元正态分布，将P(x1,x2,x3)耦合在一起了，导致逻辑函数中也是耦合的

所以要想解耦就得从正态分布上解耦

开始解耦：

最简单的方法是假设x1与x2相互独立，那么P(x1,x2)=P(x1)*P(x2)

因此这样就将式子分解耦开来了，只要独立，即便不是正态分布也可以

小结一下：

数据缺失导致逻辑回归不能使用
不能使用的问题是多维数据(x1,x2,x3)耦合在一起
耦合的根本原因是多元正态分布P(x1,x2,x3)耦合
那么要解耦这个概率，假设多维数据(x1,x2,x3)彼此独立，这样就能达到解耦目的

那么这个多维数据(x1,x2,x3)彼此独立的可能性大吗？

答：不大，比如：身高与体重不可能独立；因此这个独立是个非常强(苛刻)的条件，这也是朴素贝叶斯适用性不强的原因之一，就是因为它太粗暴的认为这三个概率独立了，但是带来的好处就是当数据缺失时，它可以解耦，所以说没有最完美的模型

假设多维数据(x1,x2,x3)彼此独立，将这个代入公式：

再推导：

那么当我知道x时，判断分类，其实就是看P(y=1|x)与P(y=0|x)谁大谁小了

上面公式中P(x_1|y=1) P(x_2|y=1) P(x_3|y=1)是未知的，需要通过训练样本学习，将这些概率学出来

再看一下这个公式的优点：

如果x2缺失了怎么办？

那么就将P(x_2|y=1) P(x_2|y=0)忽略掉就行了，就当作不存在

那么现在就只需要求解P(x_1|y=1) P(x_2|y=1) P(x_3|y=1)与P(x_1|y=0) P(x_2|y=0) P(x_3|y=0)这些项，通过训练集来求解

比如说：x1 x2 x3是三枚不同的硬币，然后他们只有两个取值

x1=0 or =1

x2=0 or =1

x3=0 or =1

Y	x1	x2	x3
1	1	0	1
1	1	1	0
0	0	1	1
0	1	0	1

上面表格每行代表一个样本

概率可以理解为频率，即：概率最终用数字表示

P(x_1,y=1)x_1和y=1共同出现的概率

P(x_1|y=1)y=1成立后，x_1的概率

本质上是拿频率推出概率，因此通过训练样本可以把P(x_1|y=1) P(x_2|y=1) P(x_3|y=1)与P(x_1|y=0) P(x_2|y=0) P(x_3|y=0)这些估计出来，那么这个过程就没有学习反复迭代的过程了，直接拿到训练样本直接统计计数就行了，用统计的方式直接计算出来

花样扩展

这样计算概率有什么问题吗？就是样本少误差就大

比如说：我抛两次硬币，很大可能两次都抛上，基于这个样本去估计概率，正面的概率为1，反面为0

那么这个公式如何改造呢？

改造公式如下：

加入了n个样本，克服样本量少的问题

当n趋近正无穷时，Count()就不起作用了

当Count()比n很大时，Count()起作用

分子为什么是n/2要保证相加等于1

将这个公式代入例子中：

上面例子说到，实际抛出硬币两次都是正面，那么P(正)=1

代入改造的式子：假想抛出1000次(n=100)硬币，有500次正面，实际抛出硬币两次都是正面

P(正)=(2+500)/(2+1000)=502/1002约等于0.5

这样就和客观事实近似了

那么加入的这个n就是先验概率，就是主观的东西，比如看到人穿裙子，就判断该人是个女人一样，硬塞的概率，以克服样本少，而不准

概率=数据+先验

先验是主观想要的概率

数据是客观存在的数据

当数据大时，概率更倾向于客观

当数据小时，概率更倾向于主观

任何场景都要有先验

比如说面试，面试官要对我有评价

能力=面试表现+先验

当面试表现里面试时长很大，说明他收集你的信息很大，评价的越准确

面试时长很短，它就取决于先验，比如工作背景、毕业学校、工作经历

再比如：之前逻辑回归中的损失函数

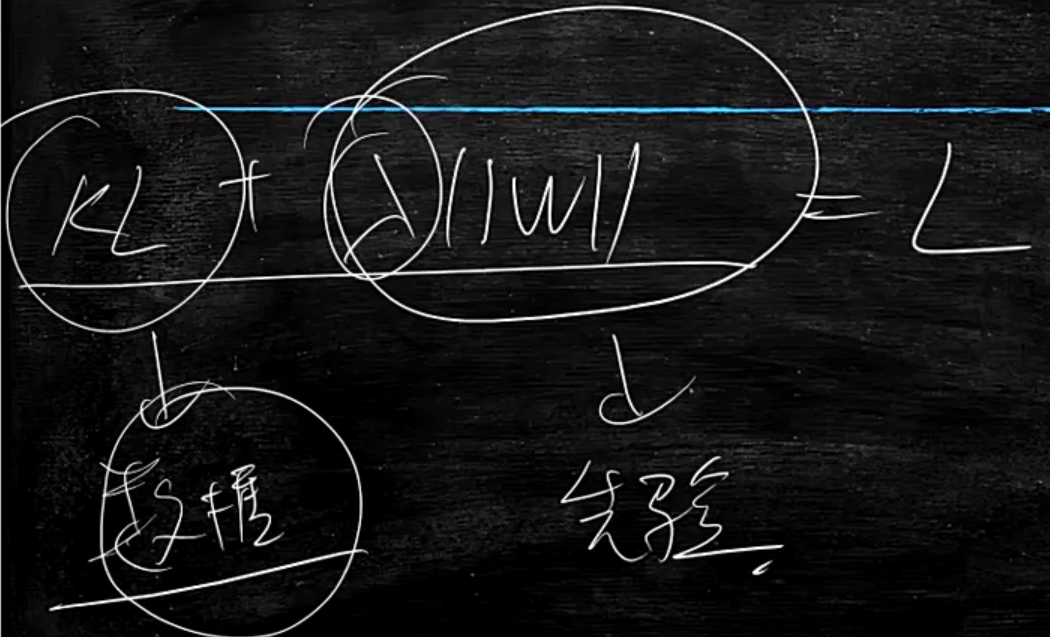
L=KL+||W||

其中KL就是数据作为支撑

||W||也能理解为是个先验

我们先验的认为这个w应该要小

总结：

逻辑回归有缺陷，不能解耦
要用频率统计概率
用频率统计概率如果样本量很小会出现概率不准的问题，解决方案：加入先验

比如：推荐系统用到先验

推荐=用户画像+内容

当我刚刚注册那个网站，还没有用户画像，那么就要从内容中的先验，即：拿最热门的数据推送给我

x1=x3将二维向量X(x1,x2)变为三维向量X(x1,x2,x3)，那么x3就是冗余项

这种操作在线性回归与逻辑回归中会影响判断结果吗？答：不会影响，可以抗冗余

那么在朴素贝叶斯中就有影响，从公式上来看多乘以一项，

从它的前提彼此独立来看，已经决定不能冗余，这也是朴素贝叶斯的缺点

像上面x取值，只有两种，不是0就是1，它的概率P(x)就是二项分布

那么有了二项分布自然就有多项分布

说到从物理意义上，判断有无均值

下图所示，右边的物理意义表达上，所以它是没有均值的，左边的物理意义表达是有均值的

男与不是男中间有过渡的状态

但是男与女它是无法平均的

所以说计算均值一定要考虑它的物理意义

再比如说：扔骰子，是比大小的，那么就有均值，

但是如果每一点代表一种状态或者决策，就没有均值

并不是所有的概率都有均值的，它的物理意义支持着它有均值才行

因此：多项分布也能通过之前的Count()来统计

若是x为连续值，那么假设(先验)它是正态分布，就是把均值与均方差给估计出来，就能把概率求解出来了

在朴素贝叶斯中，之前的那个w需要反复迭代，但在朴素贝叶斯中变为了一个统计的算法

这里要澄清：

反复迭代w并不是目的，只是手段

真正目的是找到那个合适的w，只不过没有方法可以通过解方程的办法解出来，所以才只能用不同的迭代学习的方法，在朴素贝叶斯中，已经能够一步把它搞出来了，所以就不需要用那种迭代方法了

常见的朴素贝叶斯分布和假设一般是：

二项分布
正态分布
多项分布

这三项的参数，都是通过统计出来的

代码示例(分别展示二项分布、正态分布、多项分布)：

#coding=utf-8
import numpy as np
from sklearn.naive_bayes import BernoulliNB
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
X = np.random.randint(2, size=(6, 100))  # 生成一个X[6][100]的数组，数组的值是0或者1的随机数，这[100]相当于属性值
Y = np.array([1, 2, 3, 4, 4, 5])         # Y[6]，相当于类标
clf = BernoulliNB()
clf.fit(X, Y)
print X[2:3]
print clf.predict_proba(X[2:3]) # 像这样随机生成的(独立),二值化的(伯努利分布)，推荐使用这种朴素贝叶斯
'''
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
clf = GaussianNB()            # 正态分布
clf.fit(X, Y)
print(clf.predict([[-0.8, -1]]))
clf_pf = GaussianNB()
clf_pf.partial_fit(X, Y, np.unique(Y))
print(clf_pf.predict([[-0.8, -1]]))


X = np.random.randint(5, size=(6, 100)) 
Y = np.array([1, 2, 3, 4, 5, 6])
clf = MultinomialNB()       # 多项分布
clf.fit(X, Y)
print(clf.predict(X[2:3]))
'''