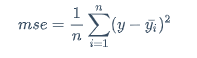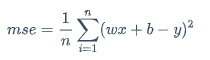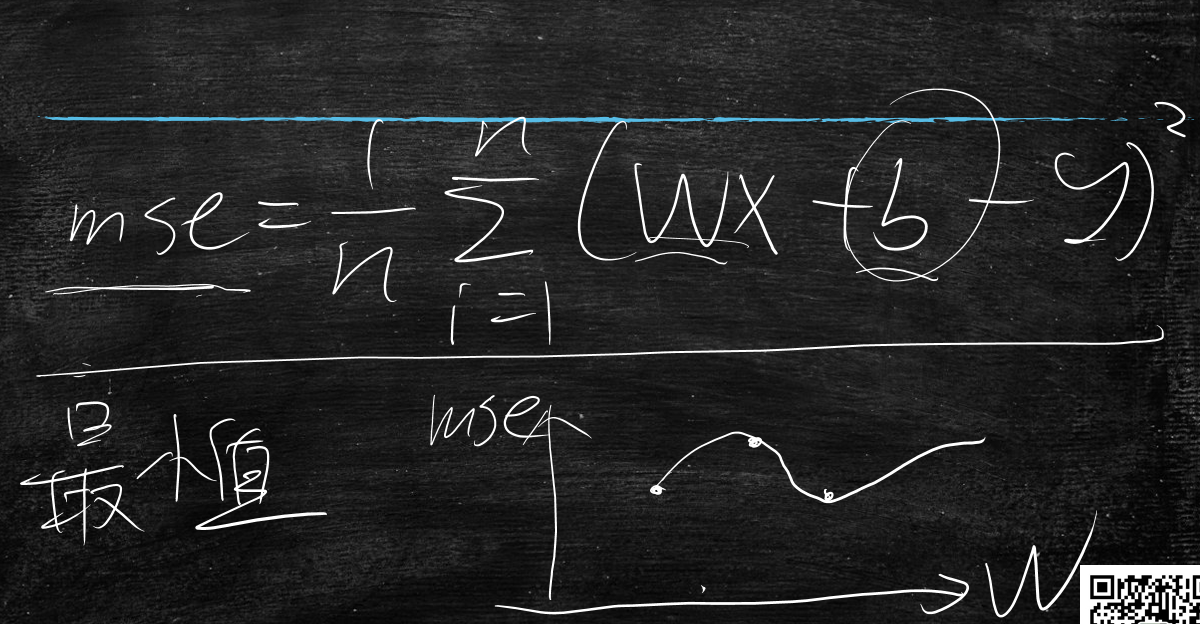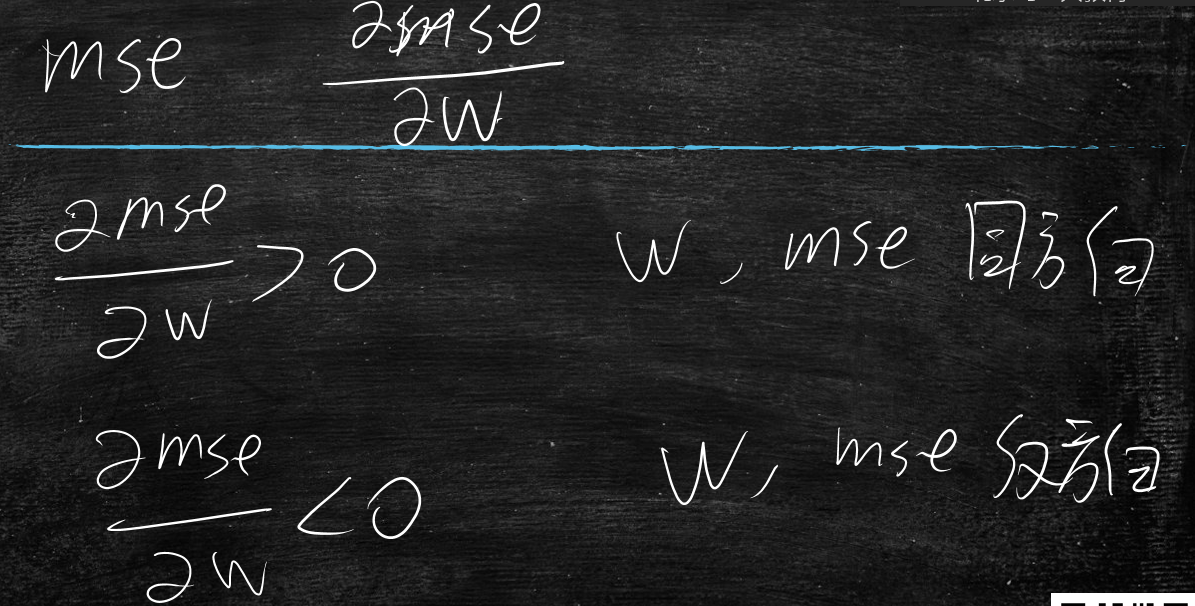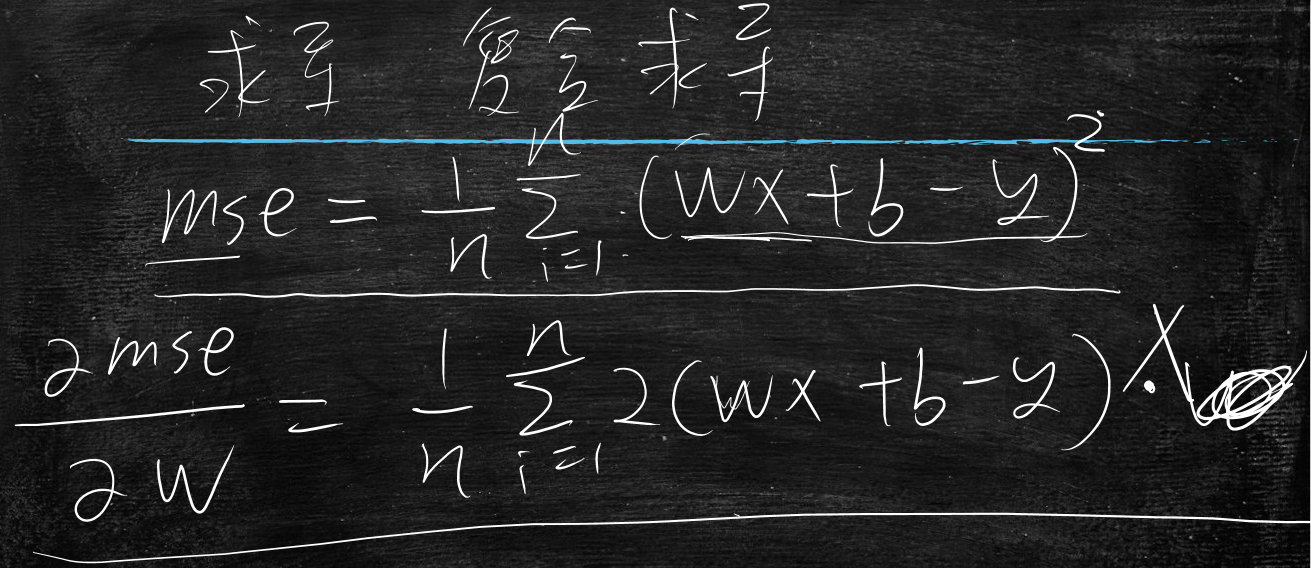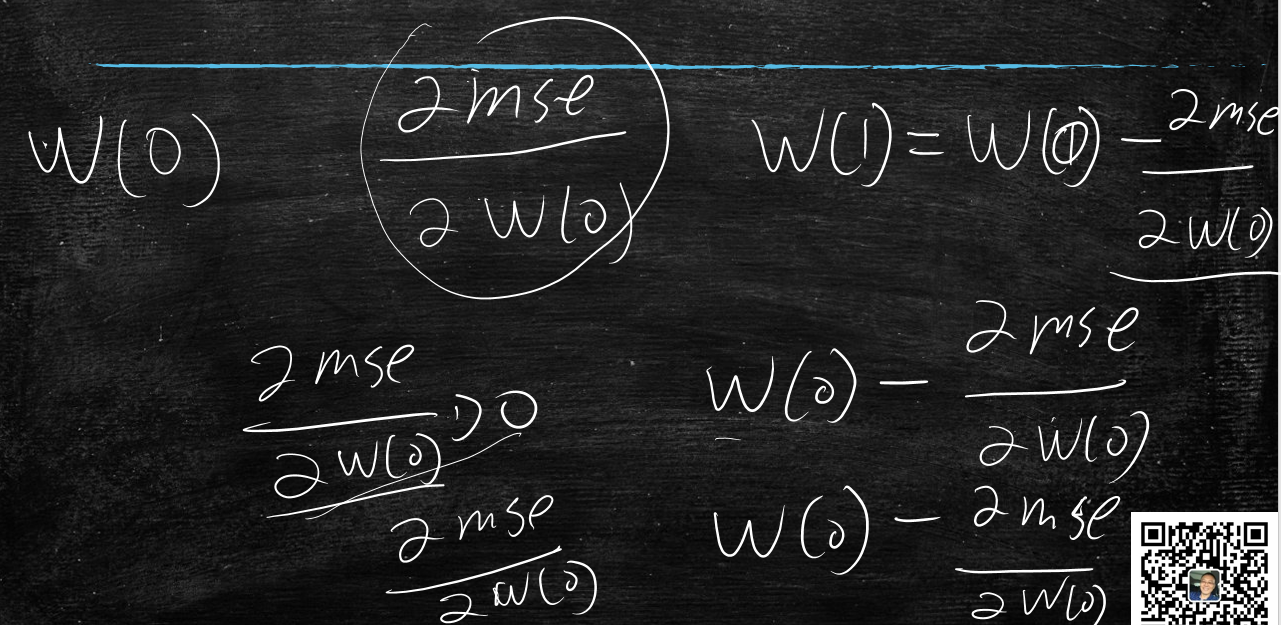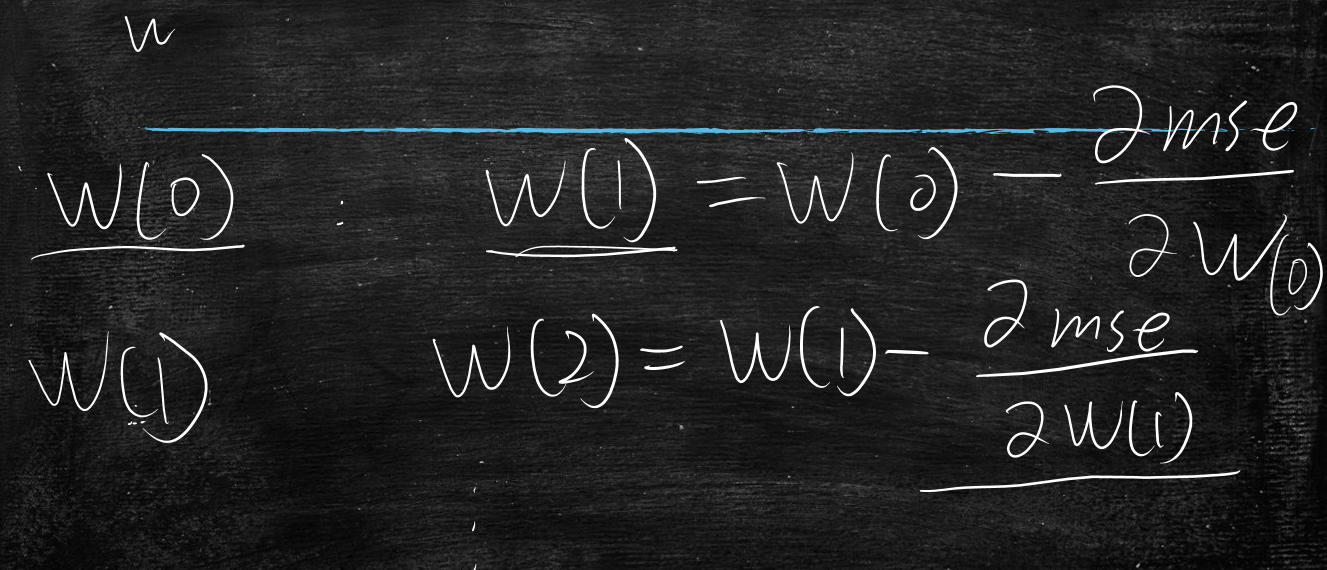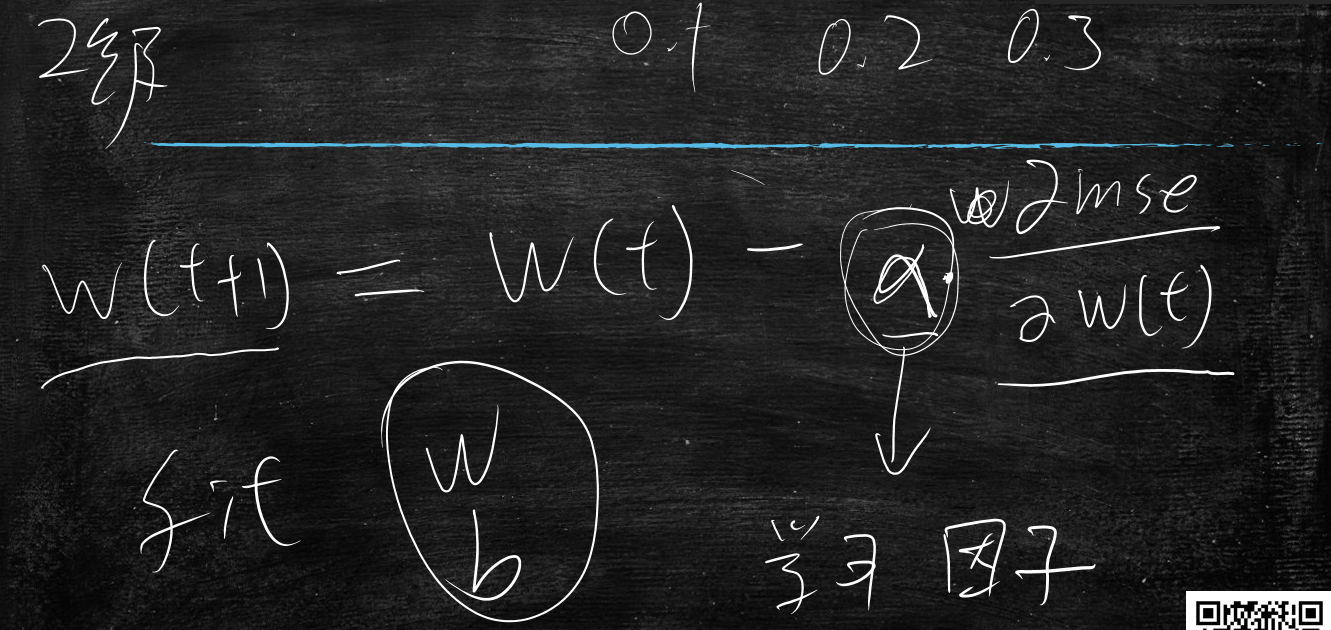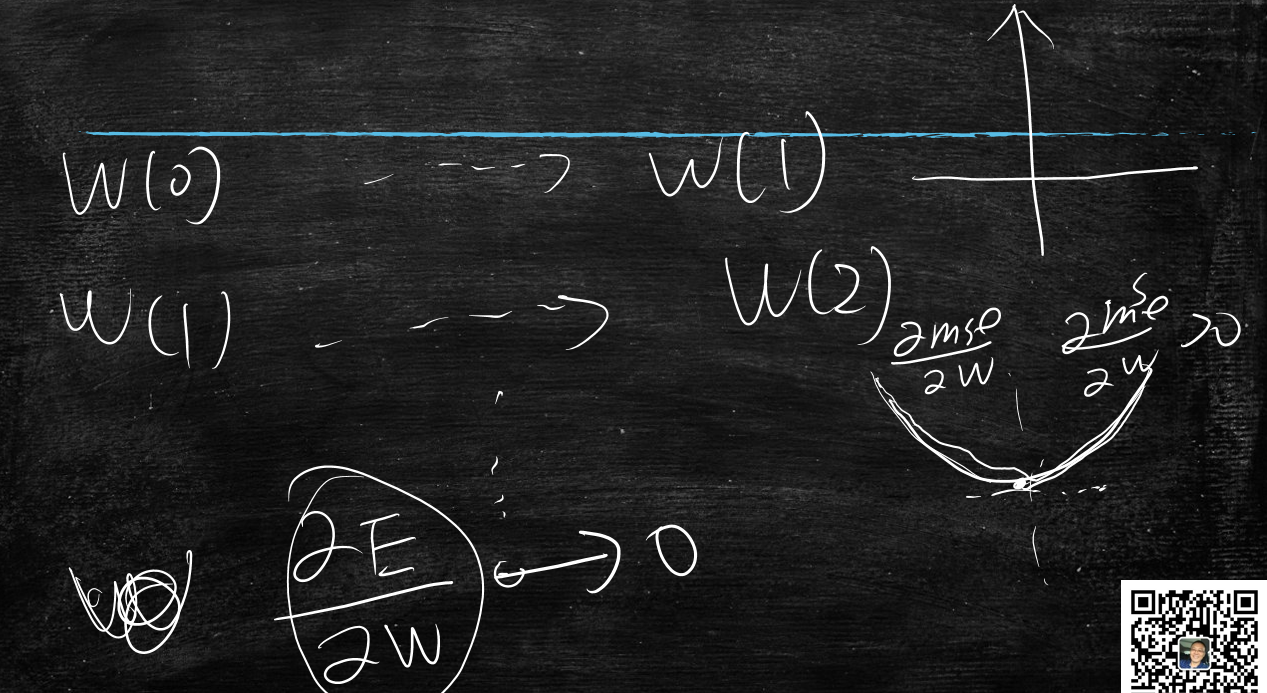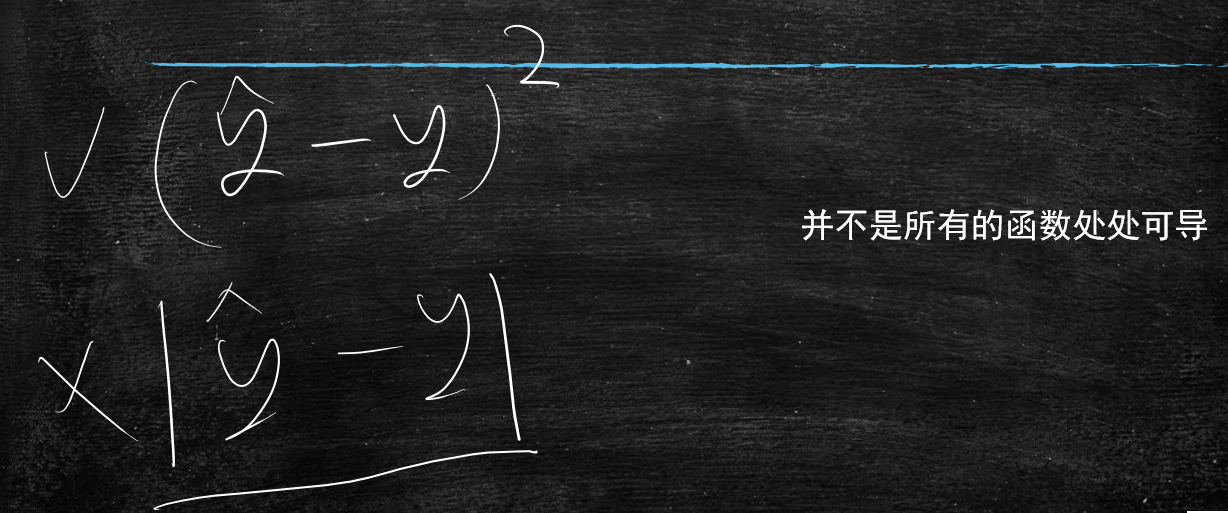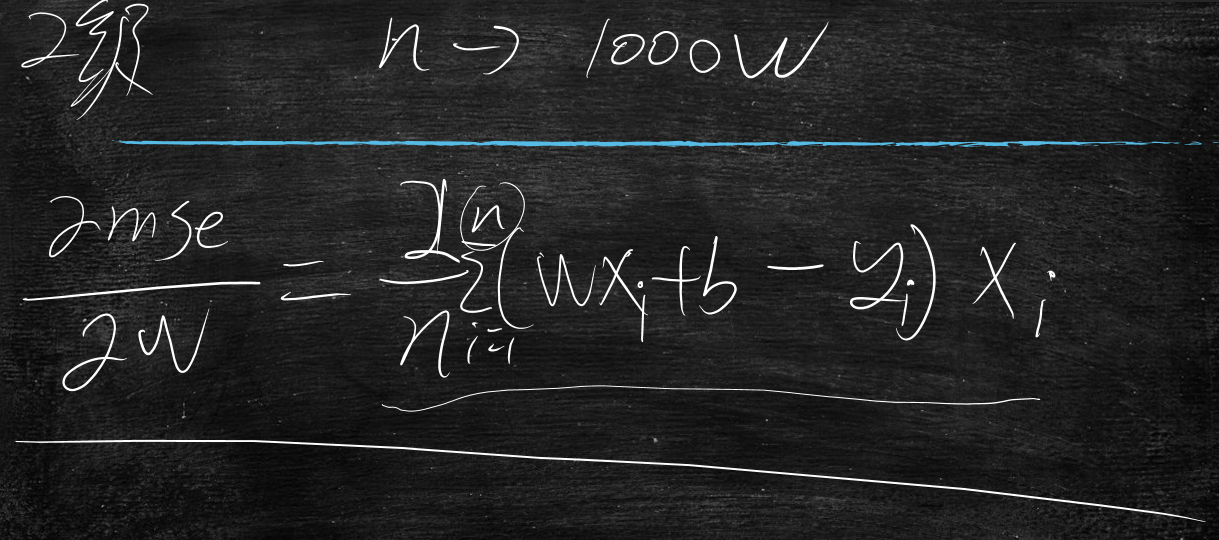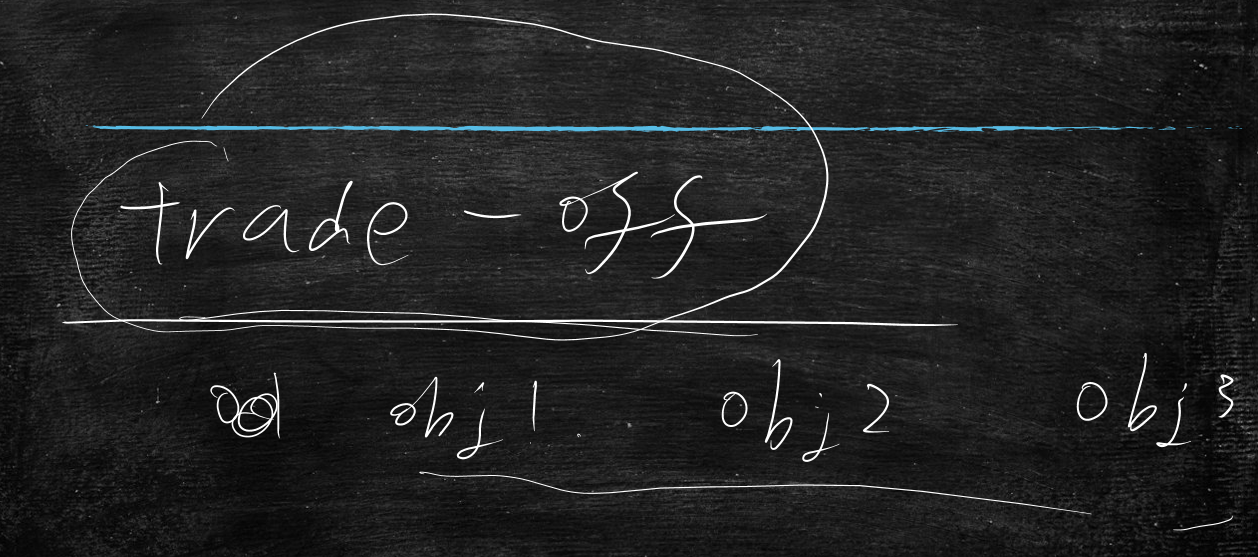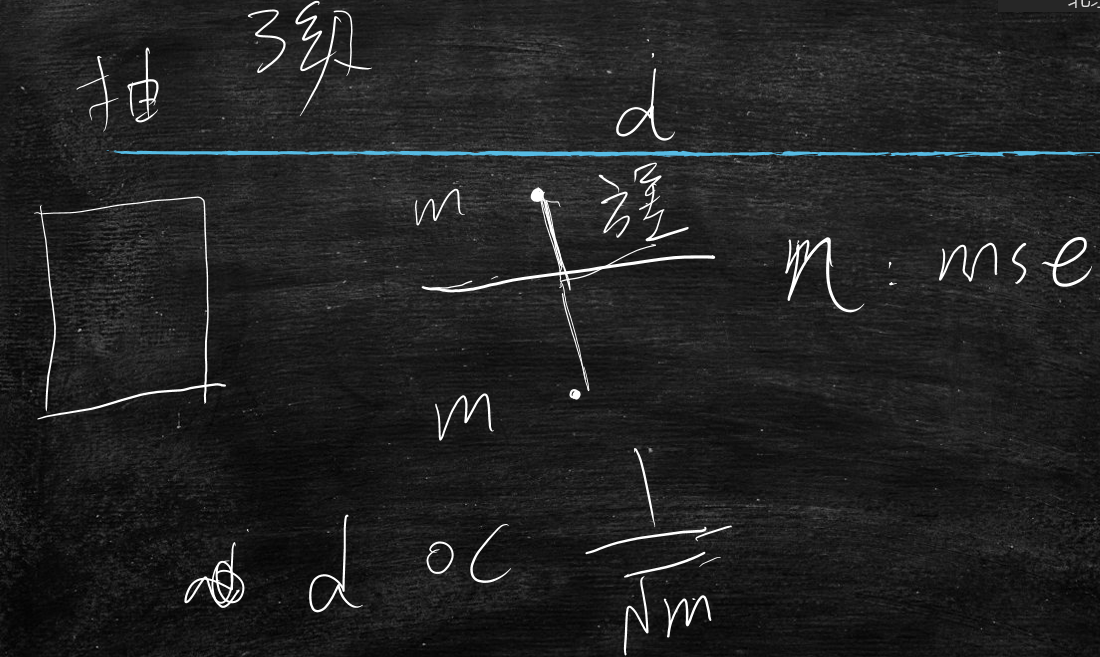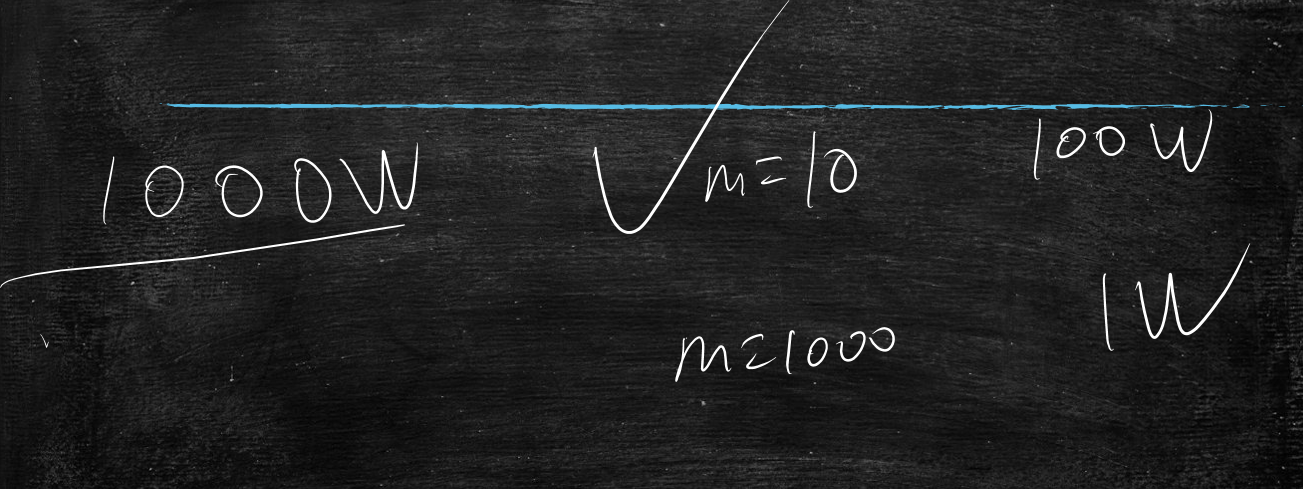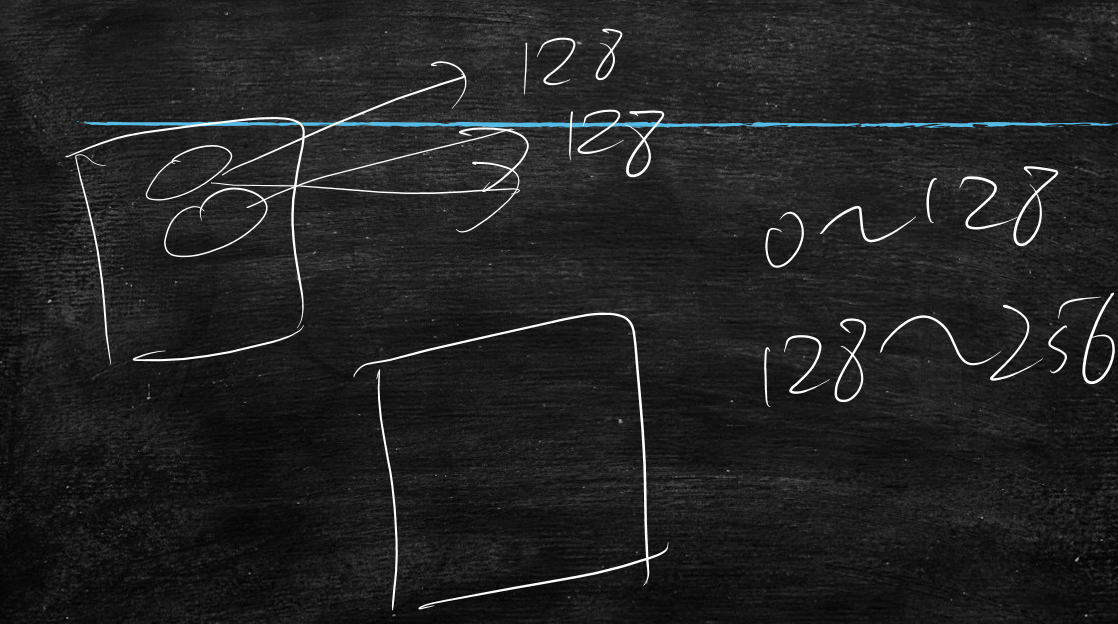# 从傻瓜到智能,梯度下降法学习法
线性回归问题转化为了求总误差最小问题
$$ mse=\frac{1}{n}\sum_{i=1}^{n}(y-\bar{y_i})^2 $$
又等价于 $$ mse=\frac{1}{n}\sum_{i=1}^{n}(wx+b-y)^2 $$
求最小,又引申出求导
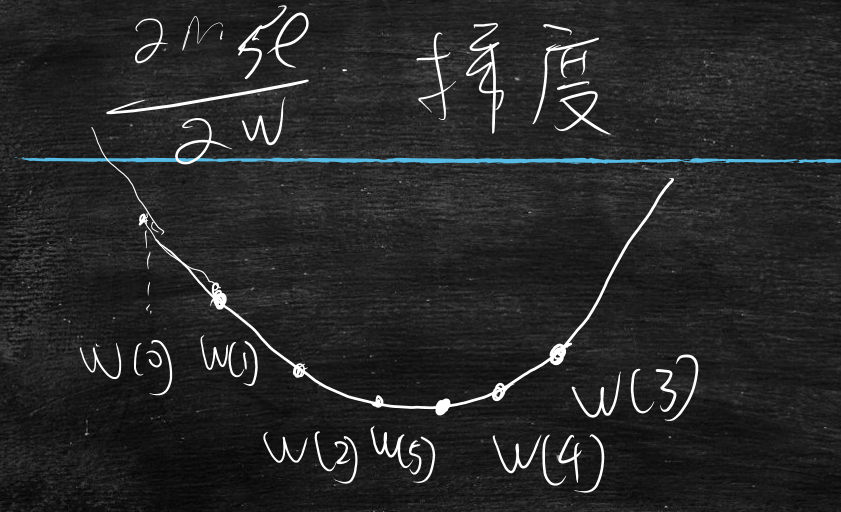
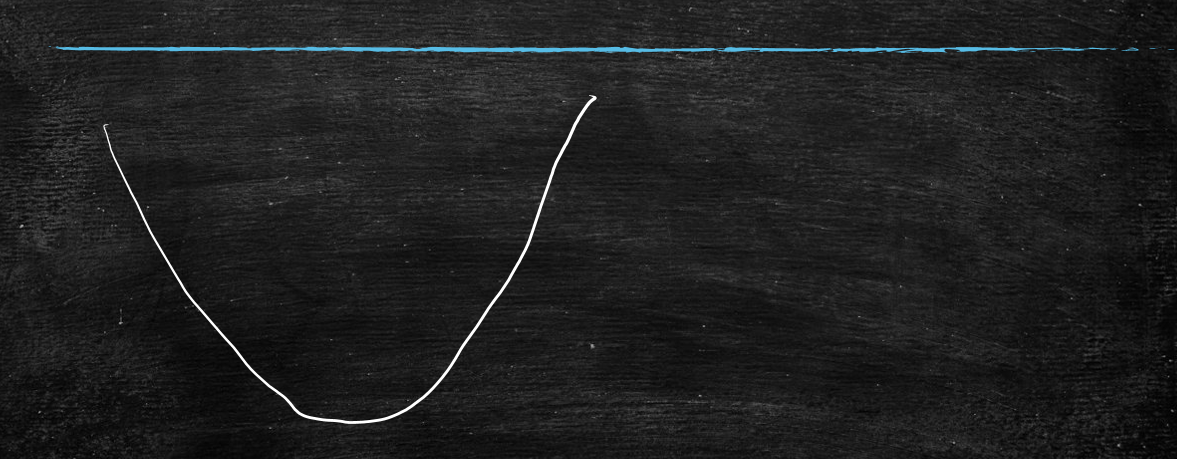
mse与w的变化曲线图表
y=wx+b 的导数:
$$
\frac{\partial y}{\partial x}=w
$$
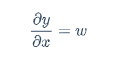
y=x^2的导数:
$$
\frac{\partial y}{\partial x}=2x
$$
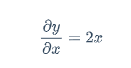
当x>0时,导数>0;当x<0时,导数<0
导数:反应mse随w变化的速率
如何找到mse的最小值?
当mse随w变化的导数>0时,w应该减小值
当mse随w变化的导数<0时,w应该增大值
复合求导过程:
$$
\frac{\partial mse}{\partial w}=\frac{1}{n}\sum_{i=1}^{n}2(wx+b-y)x
$$
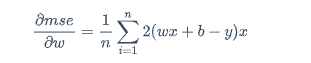
根据上述能够推导出线性回归的过程:
先随机初始化w(0),求出&mse/&w(0)的导数值
w(1) = w(0)-&mse/&w(0)
因为当&mse/&w(0)>0时,w要减小值,所以w(0)减去一个正数,值减小
当&mse/&w(0)<0时,w要增大值,所以w(0)减去一个负数,值增大
w关于mse的导数&mse/&w也是梯度,改变w,找寻mse的最小值时,就是梯度下降法
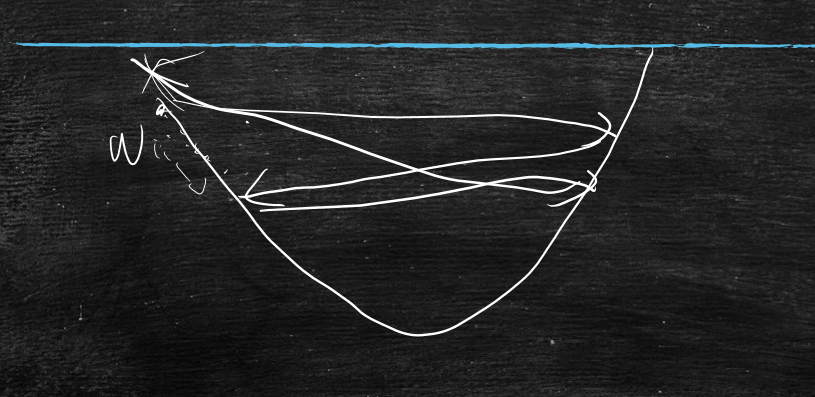
如果梯度下降的太慢(步幅太小),那么学习时间会很长
如果梯度下降的太快(步幅太大),可能会一直反复的来回震荡:
所以加入学习因子系数用来控制步幅的
当导数趋近于0时,求出最小值
但是只是通过这个也不能求出最小值,只是局部极小值,因为曲线有很多的谷,深度学习会遇到这些问题,很容易陷到局部极小
但是线性回归肯定是一个谷,只有一个最优值
回到上述结论,其实就是让导数=0,那么可以通过解方程的方式把w解出来呢?
答:可以解,但不一定能解的出,因为数据量太大了,计算机都没法算;
$$
\frac{\partial mse}{\partial w}=\frac{1}{n}\sum_{i=1}^{n}2(wx+b-y)x=0
$$
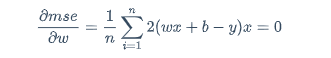
存在解,因为n过大直接解方程未必能解得出,所以需要梯度下降法,进行求解
这里说回上一节中,计算误差使用方差还是绝对值的问题
有一点原因是因为绝对值这个方程它是没有导数的,但是最主要的原因还是方差有利于注意力转移
在回头来看这个导数方程
$$
\frac{\partial mse}{\partial w}=\frac{1}{n}\sum_{i=1}^{n}2(wx+b-y)x=0
$$
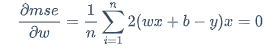
一般工程上,n一般很大,要到大概1000w数据级,这时候有什么问题呢?
就是当n很大时,这个导数算出来都非常耗时间,那么有什么折中的方案吗?
取样法,从全量训练集中抽出m个样本,近似求导
$$
\frac{\partial mse}{\partial w}=\frac{1}{m}\sum_{i=1}^{m}2(wx+b-y)x=0
$$
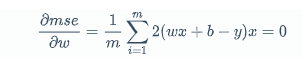
一般工程上m是2的级次幂,如16、64、128、256等,符合GPU硬件,m的导数和全量数据的导数来回震荡;
当m越小,震荡幅度大,当m越大,震荡幅度小
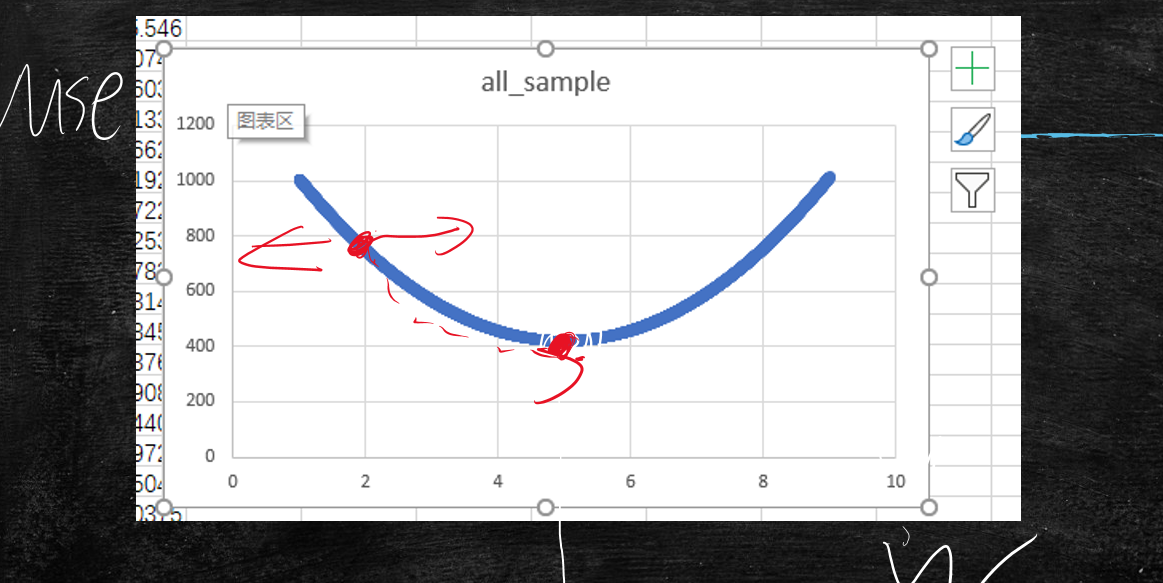
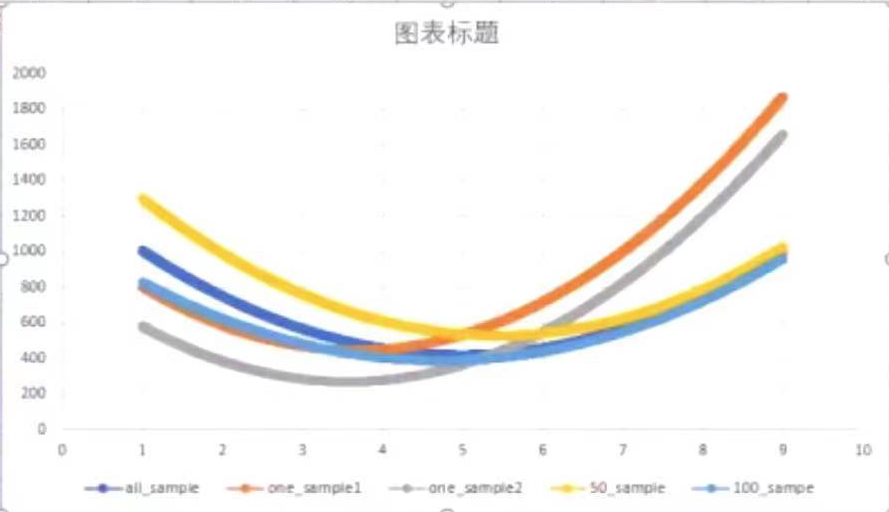
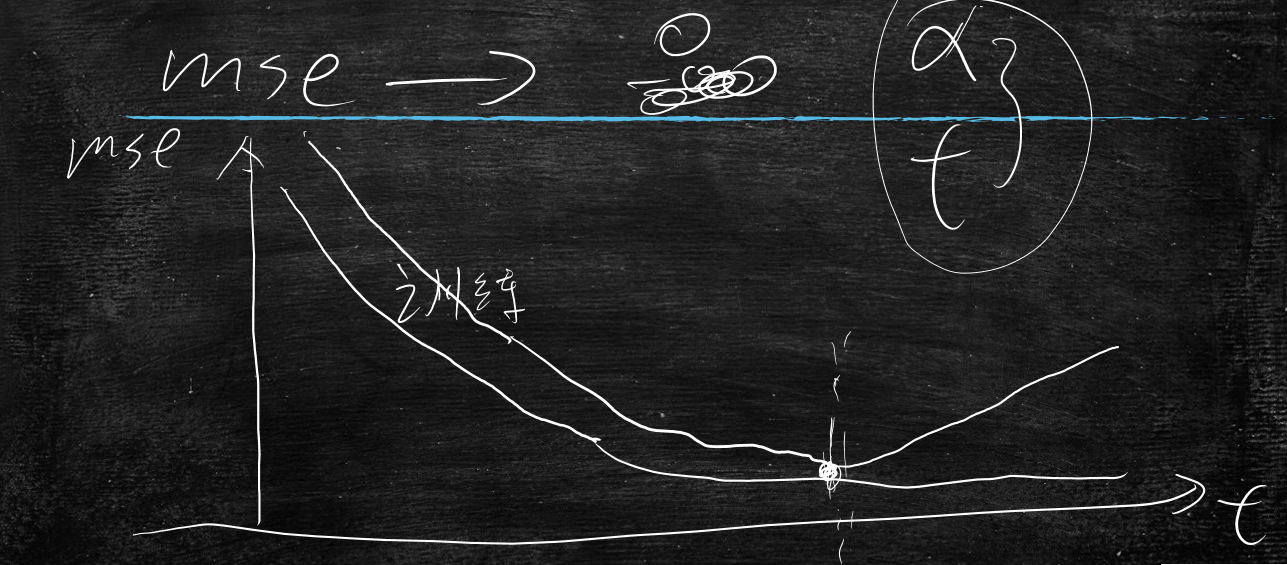
以下图表(y轴:mse;x轴:w)分别展示了
- all_sample 深蓝:全部样本数据的导数曲线
- one_sample1 橙色:随机一个样本数据的导数曲线
- one_sample2 灰色:随机一个样本数据的导数曲线
- 50_sample 黄色:随机50个样本数据的导数曲线
- 100_sample 浅蓝:随机100个样本数据的导数曲线
可以看出100样本的近似拟合全量样本的
这时就需要做trade-off权衡,两难的抉择,当mse进行优化时会遇到很多目标时,就要根据自己的经验来决策,权衡选择合适的目标值
全量样本数据n,抽样样本数据m
m的mse在n的mse上下震荡,震荡幅度(方差)为d,这个d与根号m分之1成正比
$$
\frac{1}{\sqrt m}
$$
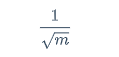
m越大那么d越小,m越小那么d越大,这个记住结论即可,推导太繁琐了
既然d与根号m分之1成正比,那么运算量是与m成正比的
那么就是说当m=100时,运算量是100,根号m分之1后是1/10
当m=10000时,运算量是10000,根号m分之1后是1/100
就是说当运算量扩大100倍后,它带来的效果才提升10倍
结论:m越大运算量越大虽然震荡的越少,但是性价比低
所以当总运算量是1000w时,一种是取10个m即m=10,算100w次要强于取1000个m即m=1000,算1w次
因此在实际中m都会取值为128或者256,取小值,多算几遍的方法
取样时可以随机取样128个,也可以把样本都编号,先是0~128、然后128~256这样顺序取也行
引申问题
训练集的mse越小越好吗?
答:不是的 要防止出现过拟合的数据,去除噪声
比如,全量数据集(all_data)中,取一部分作为训练集(train_data),在某宝算法中,收集的一条数据如下:
月薪3000元的男人 买了一个10w元名牌包,这种就是异常数据,它不是正常消费的,应该是个冲动消费,这就导致训练集数据中存在不在正常范围内的数据(脏数据),所以做训练时,是连着这块脏数据一起训练的,如果mse越来越小时,拟合特别好时,那些脏数据也学习到了,这样就学坏了,因此,在学习时,不能让它学的特好,导致过拟合,当这些点本身有误差时,若是拟合的过好,那么拿到真实环境中就会出现问题
mse随着训练时间越来越长,会学到那些脏数据的
训练集mse会随着时间越来越小,但是测试集mse刚开始会随着时间越来越小,到达极点后,反而会随着时间越来越大,所以最终要找到这个极点
就比如考试之前,我学习100个练习册(训练过程),其中有一本是错误的解法,由于我都学习记住了,但是考试(测试过程)时反而解错了
那么怎么判断学过了呢(解决过拟合问题)?
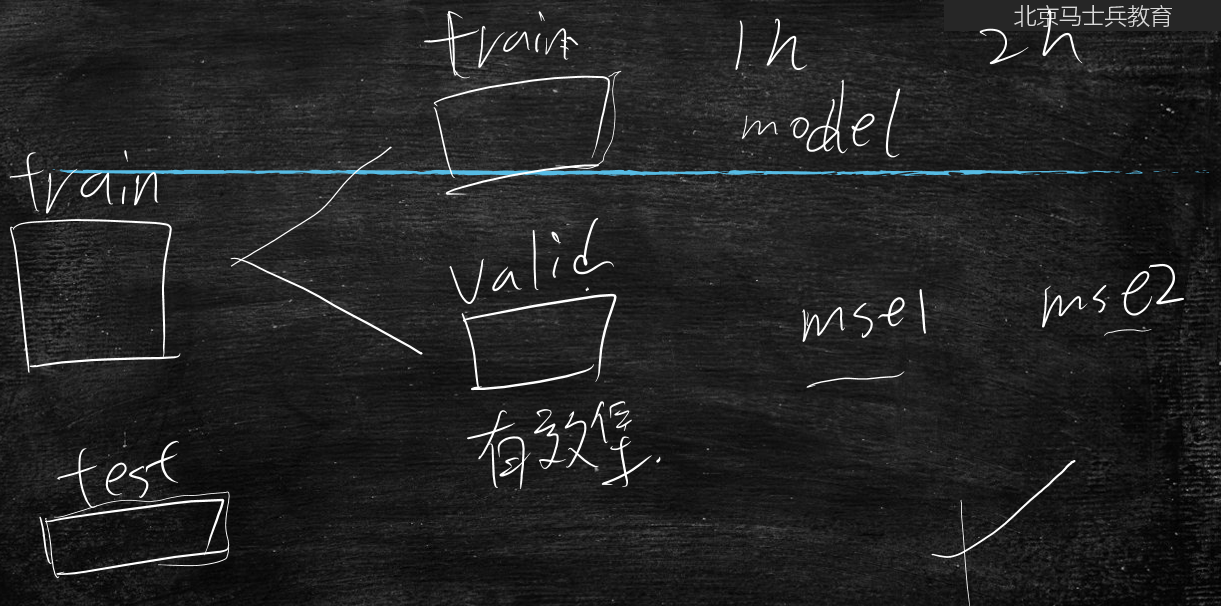
首先我们把数据先分为训练集(train_data)、测试集(test_data)
再将训练集(train_data)分为训练集(train_data)、有效集(valid_data)
在训练集上使用model模型开始训练:
当训练一个小时后得到w1时,拿到有效集上看一看得到mse1;
当训练两个小时后得到w2时,拿到有效集上看一看得到mse2;
当发现mse1开始有变大趋势时,就赶紧停止,再学就学过了
通过以上这些技术点,发现梯度下降法中的幅度系数是个调参数,而这个训练时间也是个调参数