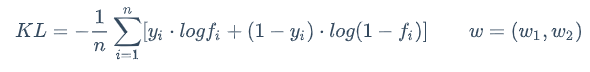ShiYu

# 让模型看的更准更稳，正则优化

回到逻辑回归

逻辑回归曲线： image-20220315215126289

image-86

w1x1+w2x2+w0=0是一条直线，用于区分坐标系中两类点的，区分圆圈与三角形

之所以使用逻辑函数：image-20220315215126289

是要让值落在0~1之间

image-86

现在让(w1,w2)取(1,1)，得出直线x1+x2=0如下图所示

那么2x1+2x2=0与-x1-x2=0也是这条直线

image-86 推出：

awx=0只要a!=0，那么a取任何值，直线都是等价的

那么既然一条直线中有无数个w的存在，那么为什么只能取一个w值呢？

这么众多的w中，有何好坏呢？

image-86 x1+x2=0这条直线，w向量是怎么表示的(与直线呈90°)，为法向量，那么一条直线有无数条法向量，反过来也是法向量，如下图所示 image-86 x=(x1,x2)也是向量，那么wx相乘就是它们的内积，内积什么时候大于0，什么时候小于0？

image-86 文字描述

θ是w与x向量的夹角

θ在-90°~90°之间，则wx>0，反之，则wx>0

从向量中，再次证明了分割线

image-86

分割线的一边是大于0，另一边是小于0，以上通过法向量解释了一遍

那么w=(1,1)与w=(-1,-1)，有什么区别？

答：最终结果的两类分，刚好把类别颠倒了

image-86 如图所示，w=(1,1)的部分>0，它的对立面则<0

w=(-1,-1)的部分>0，它的对立面则<0

image-86

那么下图所示中：

f1(x):x为正的概率

f2(x):x为负的概率

f1(x)+f2(x)=1

image-20220315222710057

image-86

推导为1：

image-20220315223056846

image-86

对于同一条直线 有无数个w的方式进行表达

对于w预测硬币的正面概率

那么-W就是预测硬币反面的概率

比如，有个分类器模型，正确率为30%，预测的w=(1,2)，但是明天你就要交活了，这时只要将w取-w，即w=(-1,-2)，那么正确率就为70%

image-86

那么以上是w取负的情况，那么w成倍的增加会发生什么情况呢？

image-86

当w->-w，w0->-w0 则 f(x)-> 1-f(x)，分类器并没有变化，只是所得分类正好相反，原先输入的是圆圈的概率，变为了三角的概率

image-86

那么当w->10w w0->10w0时，这条直线没有改变，变化的地方有哪些呢？

image-86 分析一下，代进逻辑函数

若w成倍的增加，那么-(wx+w0)会成倍的增加，最终导致f(x)的取值会发生变化，虽然不影响分类，但是会影响概率的取值，那么来分析一下取值会发生什么变化？

通过曲线分析，若是同一个x下的w成倍增加时，那么f(x)会更趋近于0或者1(两极分化更厉害)，会让取值变得很硬，w越大，取值越趋近于0或者1，这样不好，分类结果特别硬

image-86

当w=1 p1=0.6 p2=0.4

当w=100 p1->1 p2->0，这样分类结果很硬，没有中间的过渡区分度

所以得出结论，当直线没有变化时，w变小，会比较好

image-86

第二种解释：

image-20220315230147428

如果w1很大，那么x1的细微的抖动，将会使最终结果变化很大，因为w1将这个w1x1这个信号放大了

从这个角度来说，也是希望w变小，越好

image-86

第三种解释：

image-20220315230147428

比如x1的信号是真实的身高，x1的噪声是测量误差，其中噪声是随机产生的，值可大可小，满足正态分布

x1=信号+噪声

image-86

由上，每个x都能拆成信号与噪声就能写成：

image-20220315231259367

假如，这些特征相对较多时，那么当w成倍增加时，会将信号与噪声同时放大，但是由于信息冗余，当维度过多时，信号中的后面的维度会跟前面的维度大概率会冗余，比如10维->7维，但是噪声不冗余，还是10维

所以虽然信号与噪声同时放大，但是噪声是很独立的，没有冗余，所以噪声会增加的更多，w越大，性噪比会越来越小

结论：在不改变直线的前提，w越小越好

image-86

第四种解释：

机器学习模型，为的就是在测试集上表现好

把这个分解为两种目标

  1. 在训练集上表现好：就是让损失函数(KL)最小
  2. 训练集与测试集差别小

image-86

如何做到训练集与测试集差别小呢？

不考虑分类效果，单纯让它们差别小有什么办法？

答：随机猜，不管什么集(忽视数据)，全靠蒙，这样就很接近

那么当w变为什么值，f(x)值随机蒙呢？

答：w=0,那么x不管是什么(忽视数据)，f(x)=0.5，由此可见，w=0时，训练集与测试集差别最小，那么w=0也是w极端小的一种情况，从而证明当w变小时，训练集与测试集差别变小

image-86

在推理：

KL损失函数越小让训练集表现越好

||W||测试集与训练集差异小

image-20220315234846572是个系数，调节KL与||W||的比例，是侧重于KL，还是侧重于差异

若image-20220315234846572是0，则退化为最初学习逻辑回归时，完全不考虑测试集与训练集的差异，只考虑训练集的情况

若image-20220315234846572趋近于正无穷时，那么完全不考虑训练集的效果，只考虑测试集与训练集的差异

image-20220315235047685

image-86

一般来说训练集种数据量越大，越接近全量数据，那么考虑差异性就会降低，image-20220315234846572越小；数据量越小，那么考虑差异性就会提升，image-20220315234846572越大

image-86

image-20220315235047685

如果已经找到了w进行正确分类，把w扩大了2倍，损失函数(KL)会更小

其中损失函数就是让f在正确分类下越来越硬，让f更趋向于1或者0

比如：找到了一个w=(1,2)能够正确分类了，此时把它放大十倍，w=(10,20)，那么KL损失函数值会更小

因为KL损失函数就是该点概率到1或者0的距离值，当w变大，导致f更趋向于1或者0,从而使该距离变小

那么当我们单纯只拿这个KL来训练时，会导致训练的w越来越大，最终导致w值溢出

image-86

w->无穷

image-86

使用sklearn做逻辑回归时，它的损失函数就是这样的

image-20220315235047685

已经帮你自带上了这一项image-20220316001521803，因为不带这一项w根本学不出来，会导致溢出，这一项用来限制w的长度

image-20220316001521803这一项会让w越来越小

image-20220316001806571这一项会让w越来越大

所以这两项会互相牵制，彼此成就

image-86

一般来说：

image-20220315235047685

image-20220316001521803这一项叫正则项

正则项的作用：

  1. 从机器角度考虑：抑制w在分类正确情况下，按比例无限增大
  2. 减少测试集和训练集的差异性
  3. 破坏训练集的效果

image-86

image-20220316003042259这一项是衡量w的长度，有两种衡量方式：

第一种：L2正则

image-20220316003542571

第二种：L1正则

image-20220316003552175

一般没人用L3、L4正则，一般L1、L2就到头了

image-86

相当于一个衡量三角形的斜边L2

一个衡量三角形的直角边L1

image-86

这个正则项，不光用在逻辑回归，也用在线性回归

如果是L2正则时，叫做岭回归

image-86

L1和L2正则有什么区别？

关联到之前所学MSE中使用方差与绝对值

image-86

L1正则

比如w1x1+w2x2=0是条直线，两维特征，x1是身高，x2是体重，x1这个维度重要，x2这个维度次要

那么使用L1正则时，会将w2=0，将w1减少的小一些，这样影响最小

image-86

比如，向量w1=(3,2)非要减少2个长度时，会趋向于w1=(3,0)，把最差的维度趋向0，要比把每个维度都减少要好，既然一定要牺牲分类效果了，就是w1要变小时，那么就先把最差维度的牺牲掉，这样对分类效果影响最少

image-86

模型如何判断x1与x2哪个重要？

答：这个涉及统计学，模型会看每个x的分布情况，从而做出判断

比如：在训练集中，模型发现对于真实结果为1的所有样本中，x2没有x1集中，那么x2相对x1就是次要的

image-86

L2正则

image-20220315235047685

分析：当w变小，KL变大

image-86

比如：单纯只看w1减少时，KL与L2的变化情况，对于KL增加是比较稳定的，线性的，每次相对稳定的增加a，但是对于L2变化则是当w1减少到一定程度后，趋于平缓，收益变小，也就是说当w1降到一定程度后，就不再下降了，转移到w2或者其他维度了

下表所示

W1变化 KL变化 L2变化
5~4 a 25-16=9
4~3 a 16-9=7
3~2 a 9-4=5

image-86

结论

使用L2正则：w各维度普遍变小

使用L1正则：牺牲最不重要的维度

image-86

代码中使用L1或L2正则

# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from numpy import shape
from sklearn import metrics
import numpy as np
def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
 
def train_model(reg):
	print reg
	model = LogisticRegression(penalty=reg)
	model.fit(X_train, y_train)
	print "w", model.coef_
	#print (model.intercept_)
	y_pred_train = model.predict(X_train)
	y_pred_test = model.predict(X_test)
	e_train=metrics.mean_squared_error(y_train, y_pred_train)
	e_test=metrics.mean_squared_error(y_test, y_pred_test)
	'''
	print "训练集MSE:{}".format(e_train)
	print "测试集MSE:{}".format(e_test)
	print "训练测试差异{}".format(e_test-e_train)
	print
	'''
#train_model(reg="None")
train_model(reg="l1")
train_model(reg="l2")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

执行结果

image-20220316094526143

从上图看出，使用L1正则，w有很多项变为0，从而达到降维的效果

代码中不指定penalty(惩罚)项时，默认是L2正则 那么要是需求上要求降维时，不能想当然的把权重小的直接拿掉，因为存在信息冗余的问题，应该使用L1正则降维，因为如下图所示，将w1变为0，但是w3变为0.6

image-86

一般情况下使用L1正则居多，因为不但能起到降维效果，也能提高泛化能力

模型最终想要的是：测试集效果好

而使用机器学习，首先保证训练集效果好，然后再使得训练集和测试集差异小，

其中训练集效果好就是我们的损失函数小，

训练集和测试集差异小就是说模型的推广、泛化能力强

image-86

L2正则：数学完美，实际很少用到，或者没有降维需求时，可以使用L2正则

image-86

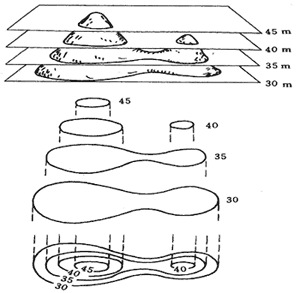
等高线指的是地形图上高度相等的相邻各点所连成的闭合曲线。把地面上海拔高度相同的点连成的闭合曲线，并垂直投影到一个水平面上，并按比例缩绘在图纸上，就得到等高线。等高线也可以看作是不同海拔高度的水平面与实际地面的交线，所以等高线是闭合曲线。在等高线上标注的数字为该等高线的海拔。

图1

特征

1、位于同一等高线上的地面点，海拔高度相同。但海拔高度相同的点不一定位于同一条等高线上。（如上图140m的等高线）

2、在同一幅图内，除了陡崖以外，不同高程的等高线不能相交。

3、在图廓内相邻等高线的高差一般是相同的，因此地面坡度与等高线之间的等高线平距成反比，等高线平距愈小，等高线排列越密，说明地面坡度越大；等高线平距愈大，等高线排列越稀，则说明地面坡度愈小。

4、等高线是一条闭合的曲线，如果不能在同一幅内闭合，则必在相邻或者其他图幅内闭合。

5、等高线经过山脊或山谷时改变方向，因此，山脊线或者山谷线应垂直于等高线转折点处的切线，即等高线与山脊线或者山谷线正交。

只考虑两维的情况下

image-20220316101558889

下图中的等高线图：

圆圈线上的点代表：w1,w2

等高线的高度代表：那一点上的w1,w2的KL距离

当w一直变小，KL距离变大，越来越高

image-86

image-20220316105051238

由于x1比x2的数据量级大，当w变小时，w1变化小一定数值，要比w2对于KL贡献大，也就是w1变化时，等高线会变陡

image-86

所以当x1量级大于x2的时候，我们希望学习的时候w1变化慢一点，而w2变化快一点

损失函数：

KL对w求导：

image-20220316112510777

image-86

image-20220316112510777

分为两种情况：

y=1有a个样本

y=0有b个样本

公式转化为：

image-20220316143809385

当f趋近于0，就说明负样本这一类已经分好了image-86

那么只需要看前面部分image-20220316151200089从这个式子中能看出

当x1数据量大时，导数变大，w1变化的快，

当x2数据量小时，导数变小，w2变大的慢；因为导数是反应变化率

image-86

在通过梯度下降法求证：

image-20220316155707692

通过分析公式：x1大，则w1变化大，x2小，则w2变化小

image-86

但是上面理想情况等高线的分析：当x1量级大于x2的时候，我们希望学习的时候w1变化慢一点，而w2变化快一点，而实际情况则是x1大，则w1变化大，x2小，则w2变化小

也就是说实际的梯度下降过程中是有问题的，那么有什么办法解决呢？

分析造成上述问题的本质原因是x1与x2的数据量级不一致，造成理想与实际的差异大

那么我们把数据量级变一致就行了，就是归一

如何归一呢？

有很多样本(x1，x2)，先来看一维

取很多样本中的x1里面最大值max1，最小值min1，将x1代入如下公式：

image-20220316160605245

这样x1的取值范围就在0~1之间，这样便将数据量级变为一致了

但是这样做是有问题的

image-86

脏数据或者是噪声，影响会很大

比如：月薪，有1w，2w，3w，突然来个首富，1000w

那么通过上面公式取值方法：那么月薪1w、2w、3w的就挤在一起了，没有差异了，信息损失了，区分度下降

image-86

所以一般不用上面的方法

一般使用均值image-20220316160922763、均方差image-20220316160947924

x1围绕均值左右分布，当x1的数据量很大时，均方差变大

image-20220316161439713

image-86

上面对x向量的这种特殊处理，在机器学习中叫做对输入样本的正规化，对输入数据做预处理，可以使模型学习的更好

那么对输入数据进行预处理会改变最终的学习结果吗？

理论上说：预处理是不会对最终理想结果进行改变的

但是实际上输入数据正规化后，让学习加速，在同样的时间内，比如只训练一个小时，得出的改善的结果，因为理论上的结果需要花费很久的时间去学习才能够学到，所以正规化是非常有必要的，能够加快学习速度

image-86

正规化如何加快学习速度呢？

正规化之前，由于w1梯度下降步幅大于w2，就会如下图所示，来回反复震荡，才最终走到圆心处

image-86

正规化后，之前椭圆线趋近于圆线，w1与w2的幅度是一样的，那么w很快就能下降到圆心处

image-86

损失函数：

y=1有n个样本

y=0有m个样本

KL对w求导：

image-20220316164001888

当f趋近于1时，那么加号前面的趋近于0，说明正样本已经基本学完了，开始学习负样本的了

image-86

那么就能把情况简化一下：

image-20220316164648526

image-86

image-20220316164648526

当x1是身高，x2是体重时，那么都是大于0的数值

那么看这个式子image-20220316164922001，f是0~1之间的数，并且x1与x2都是大于的数那么，w则只能变小，越来越小

image-86

推理出：

w1与w2只能同时增加或者同时减少，因为x1与x2是大于0的

image-86

假如输入数据已经正规化了，那么等高线也接近于圆形了

如果w1与w2只能同增或者同减

那么w的移动范围只能是1(同增)、3(同减)象限内

既然只能是往1或者3走，那么圆心处是学习的最优点，现在w在右下方处，不能朝着2象限走，只能绕远路，先1象限一大步，然后3象限退一步，导致学习慢

造成这一问题的根本原因就是x1与x2同号

image-86

上述问题如何解决呢？

让x1与x2可正可负，引入均值image-20220316160922763

将x1待入下面公式：

image-20220316170512049

该公式就保证了x1就有正有负了

image-86

这种方式也叫做特征转换，将采集的自然信号，经过转换，不会增加信息、也不减少信息，但是可让学习加速

image-86

演示代码：使用方差与均值

from sklearn import preprocessing
import numpy as np
X = np.array([[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.]])
scaler = preprocessing.StandardScaler().fit(X)
print "mean",scaler.mean_
print "scale",scaler.scale_


print scaler.transform(X)
1
2
3
4
5
6
7
8
9
10

image-20220316171607474

总结：

输入数据向量x，经过逻辑回归LR模型，输出y（0~1）之间的概率值

模型就是通过逻辑函数不断调整w

交叉熵损失函数=KL距离

image-86

除了损失函数以外，还有L1与L2正则，提升泛化能力

还要对输入数据进行标准化(让数据可正可负)及正规化(让数据量级归一均衡)，提升学习速度

评价指标：

  1. 正确率
  2. 准确率和召回率
  3. Roc曲线 Auc值 真实反应正样本中预测分值大于负样本中预测分值的组合数

image-86

← 让学习更高效，数值优化和一只看不见的手 →