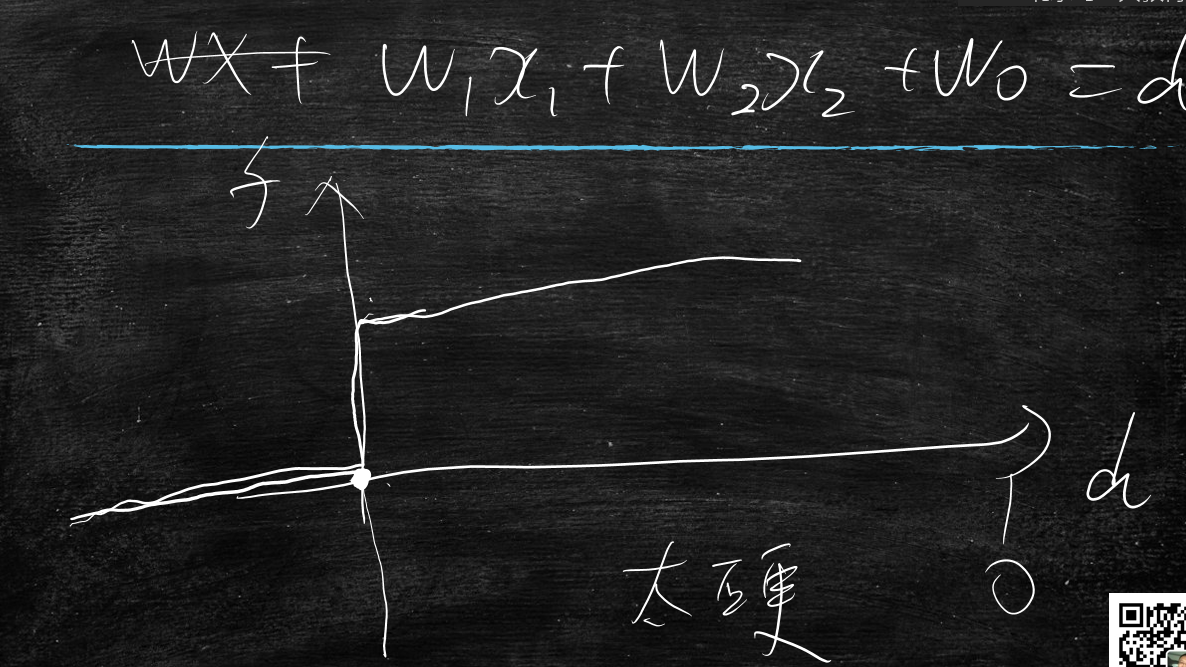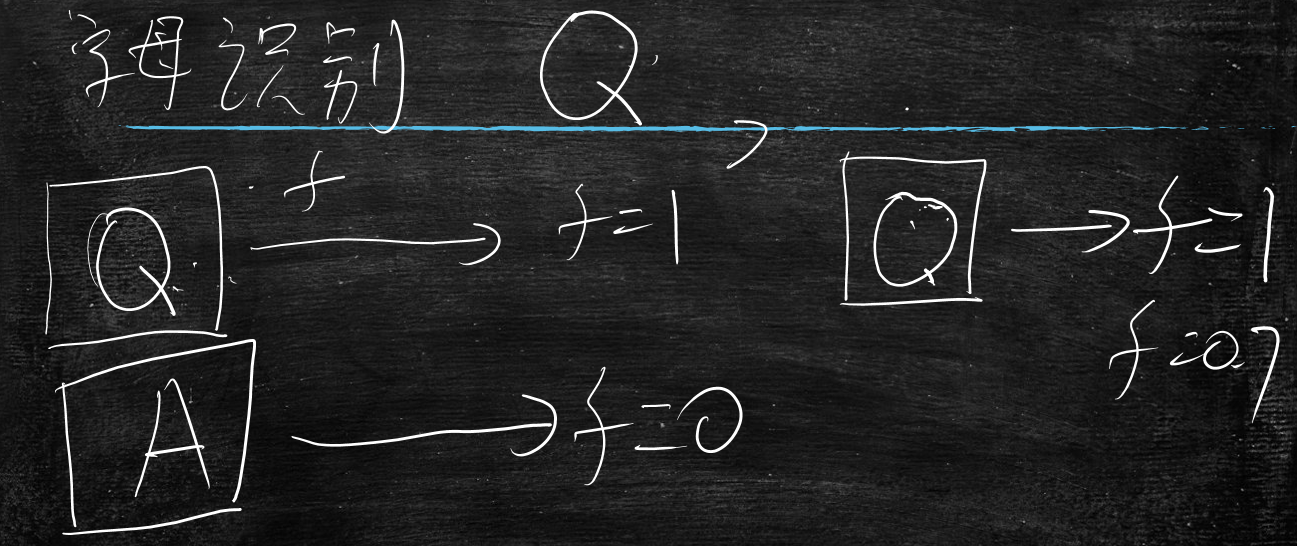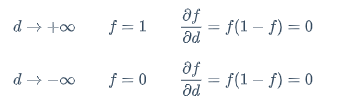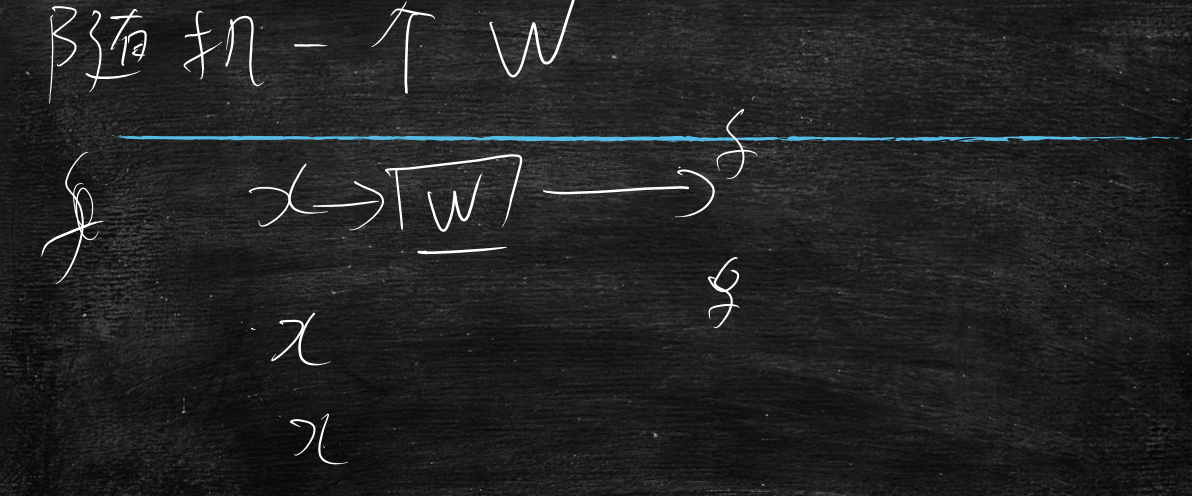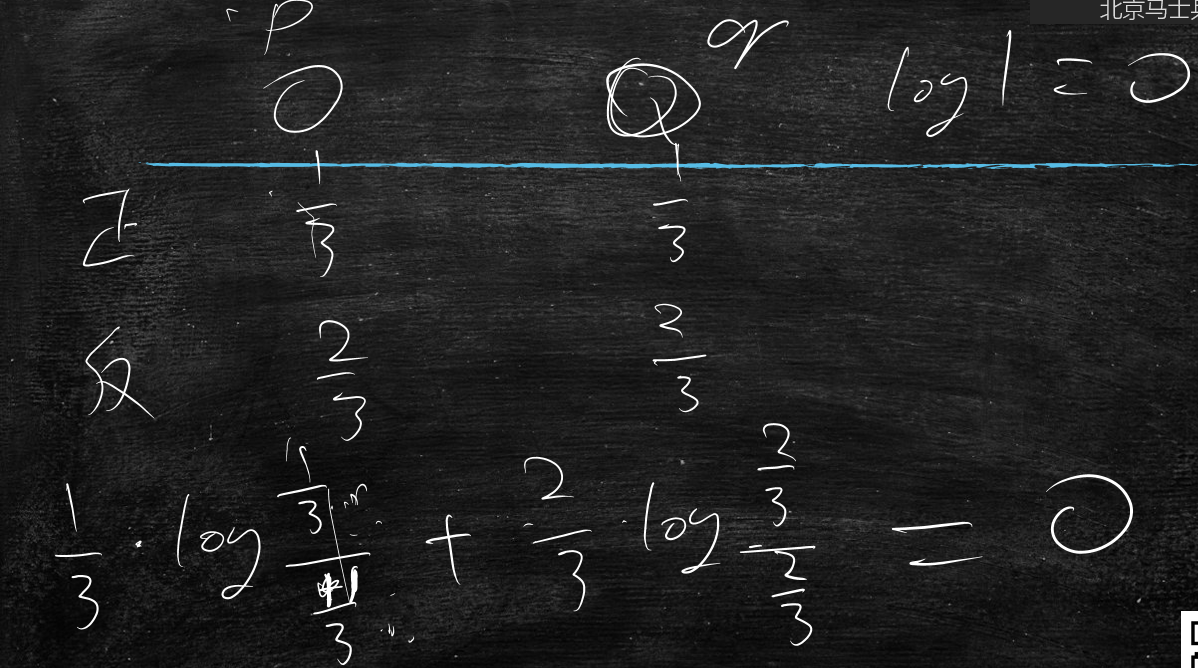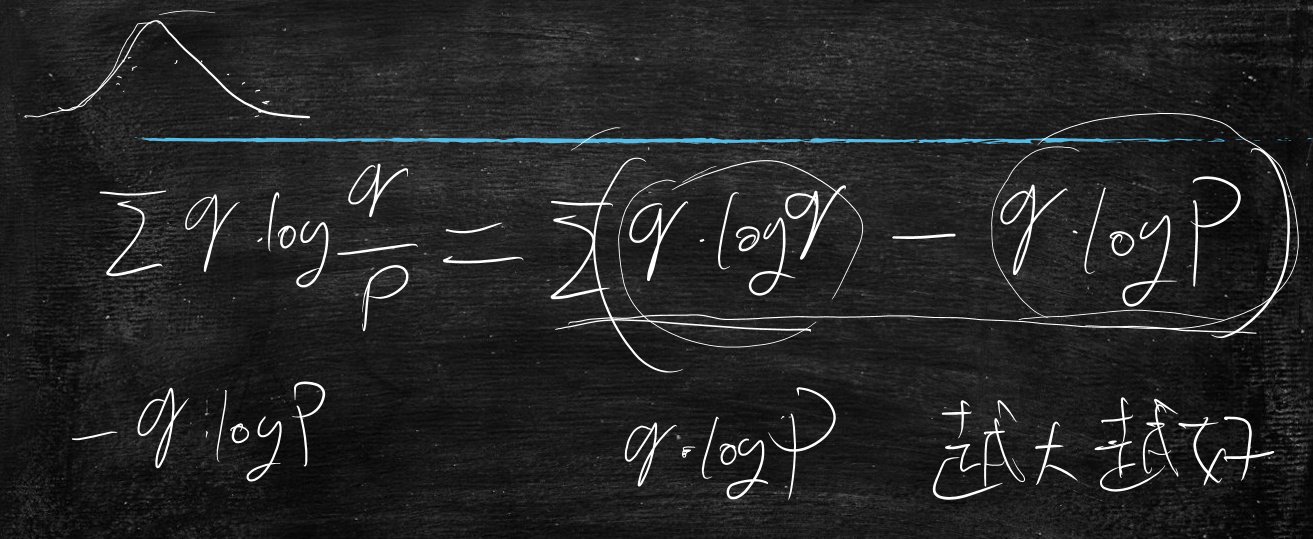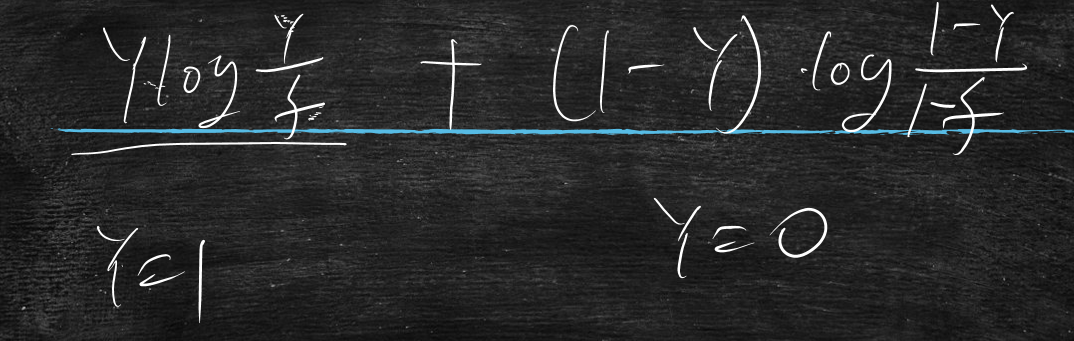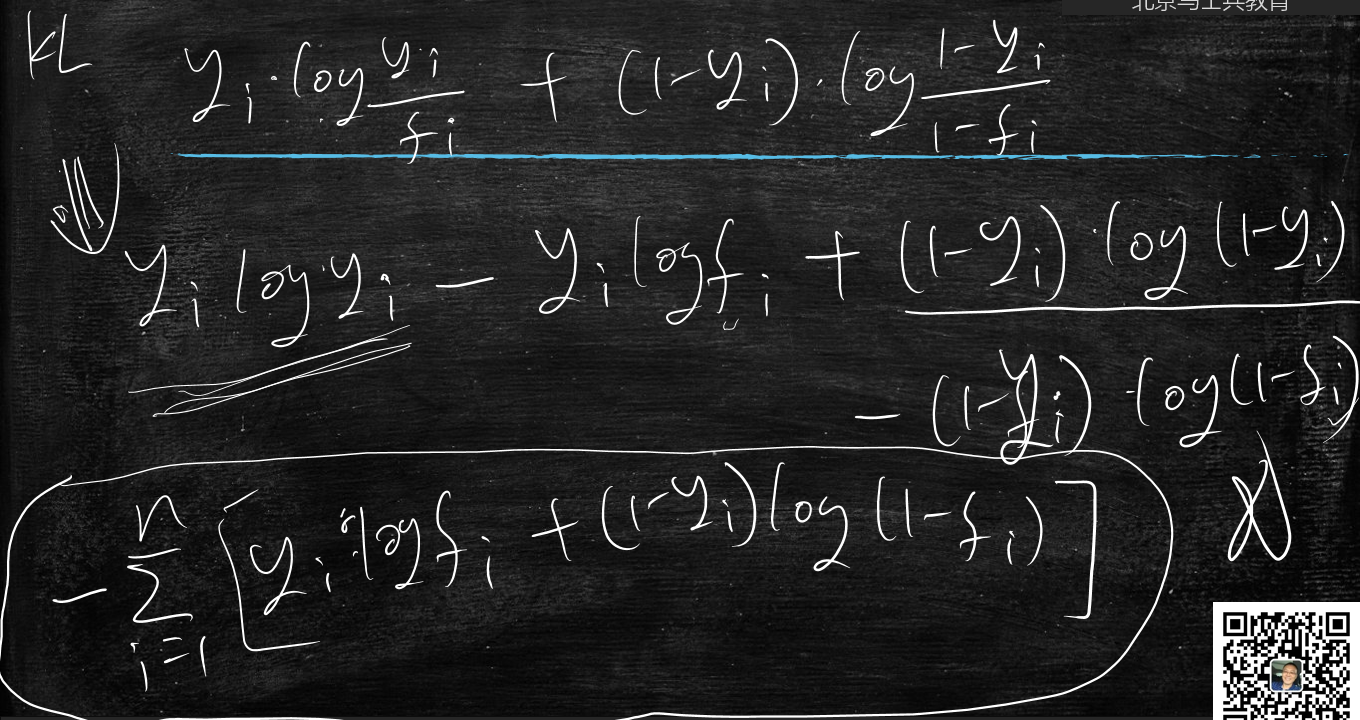# 猛将起于卒伍，工业环境下的分类模型
前言
前面2至4节讲了线性回归，从这小节开始讲解逻辑回归
从比较高度上来看，
线性回归是逻辑回归的基础
逻辑回归是神经网络(深度学习)的基础
神经网络顾名思义像人一样有很多的细胞，然后组建成非常复杂的网络，这个网络越深越复杂，所以也叫做深度学习
而逻辑回归它是某一个神经细胞，咱们先从细胞学起，把细胞掌握，后面再学其整个的网络，从细节到宏观的过程
线性回归中很多结论是可以拿到逻辑回归中用的
线性回归一般用于做预测用的，如预测股价、预测房价等
逻辑回归一般用于做分类用的，输出的是类别，如输入一张图片，分类这个图片是猫、狗、美女、男人等
又如输入一个广告和用户画像，输出用户的决策(是点击这个广告还是不点击该广告)
分类还有多分类
比如，输入1个x，输出4个y(猫、狗、美女、男人)
x表示一张图片
y表示每个分类的概率(P1、P2、P3、P4)
分类还有二分类
比如，输入1个x，输出2个y
y表示每个分类的概率(P1、P2)
那么分类里面有无一分类的概念呢？
答：没有一分类，至少是二分类
先从二分类介绍
比如，输入1个x，输出2个y
x表示一张图片
y表示是否是猫的概率(P1：是猫的概率、P2：不是猫的概率)
这里P1+P2=1
所以这个模型可以简化，我只要P1就行了，剩下的P2我用1-P1得到
所以得出结论：二分类简化一个输出的类别，前提是这两个分类是互斥的
就是说P1是猫，P2不是猫，这种互斥(P1+P2=1)的才行
反之P1是猫，P2是狗，这种不互斥的(P1+P2!=1)不行
那么开始从最简单的搞起
做二分类时，先简化为只有一个输出的情况
输入向量(x1,x2)，输出1个f
模型设计为：
w1x1+w2x2+w0>0时，f=1
w1x1+w2x2+w0<0时，f=0
那么分析这个方程式w1x1+w2x2+w0=0是条直线，那么它>0的点是在直线的上方，<0的点在直线下方，直线上的点是=0
线性回归与逻辑回归对比
- 线性回归：知道坐标的一部分，通过预测另一个
- 逻辑回归：知道完整的坐标，计算和直线的相对位置，找直线的过程
接下来再分析这个分类曲线
w1x1+w2x2+w0=d
那么d>0时，f=1；
d<0时，f=0；
那么这样的分类曲线有什么问题呢？
太硬了，f要么是1，要么是0。
比如字母识别 识别字母Q
当输入图片Q时，输出f=1
当输入图片A时，输出f=0
当输入图片长得很像Q时，期望输出f=0.7或者0.8等结果
用于区分图片Q和类似于图片Q的图片
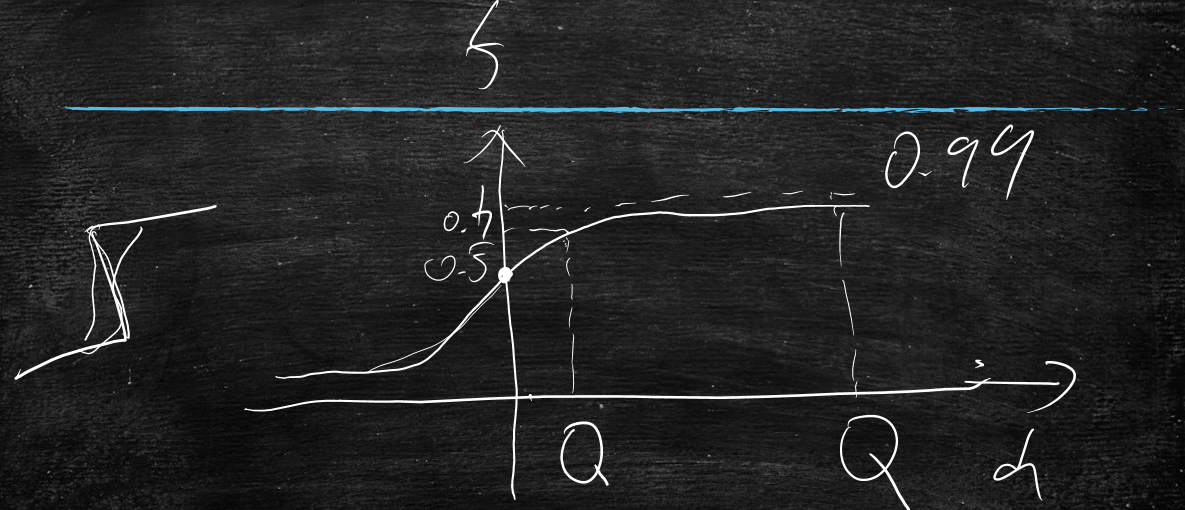
所以期望上面的分类曲线软一些，平滑一些，当d=0时，f=0.5
为了达到平滑的目的，引入方程式：
$$
d=w_1x_1+w_2x_2+w_0 \qquad f=\frac{1}{1+e^{-d}}
$$
$$
d \rightarrow +\infty \qquad f=\frac{1}{1+0}=1
$$
$$
d \rightarrow -\infty \qquad f=\frac{1}{1+\infty}=0
$$
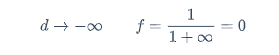$$
d \rightarrow 0 \qquad f=\frac{1}{1+1}=0.5
$$
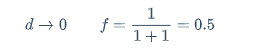
以上方程式是高斯找出来的，能够完美的达到了咱们的目的，但是不是这一种函数能满足这个目的
只能无穷的接近0和1，永远也到不了0和1
特点：
当d非常小或者非常大时，对f的影响非常小
当d在0附近时，对f的影响大
分析导数的图形如下图所示
$$
\frac{\partial f}{\partial d}=f(1-f)
$$
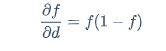$$
d=0 \qquad f=0.5 \qquad \frac{\partial f}{\partial d}=f(1-f)=0.25
$$
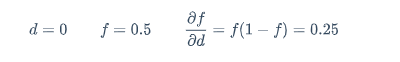$$
d \rightarrow +\infty \qquad f=1 \qquad \frac{\partial f}{\partial d}=f(1-f)=0
$$
$$ d \rightarrow -\infty \qquad f=0 \qquad \frac{\partial f}{\partial d}=f(1-f)=0 $$
导数走势图是关于0对称的
那么这个模型如何使用
将公式代入，还是不断的调整w，来影响f的值
和线性回归一样还是学习w
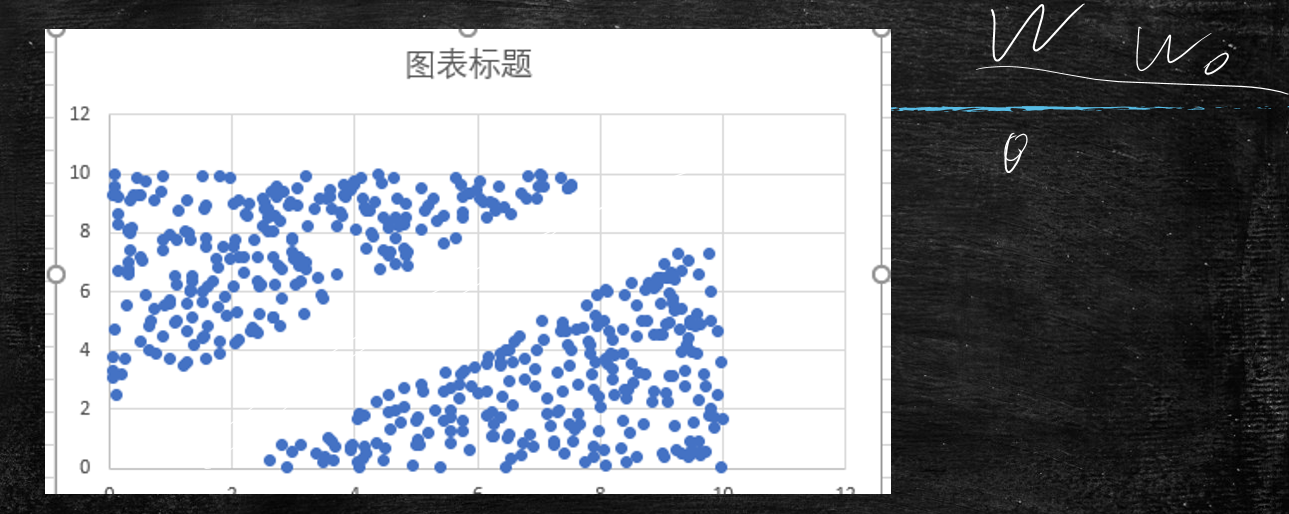
数据分布
不断的调整w，找到一条合适的直线接不同的分类分别开来，然后代进去，把概率算出来
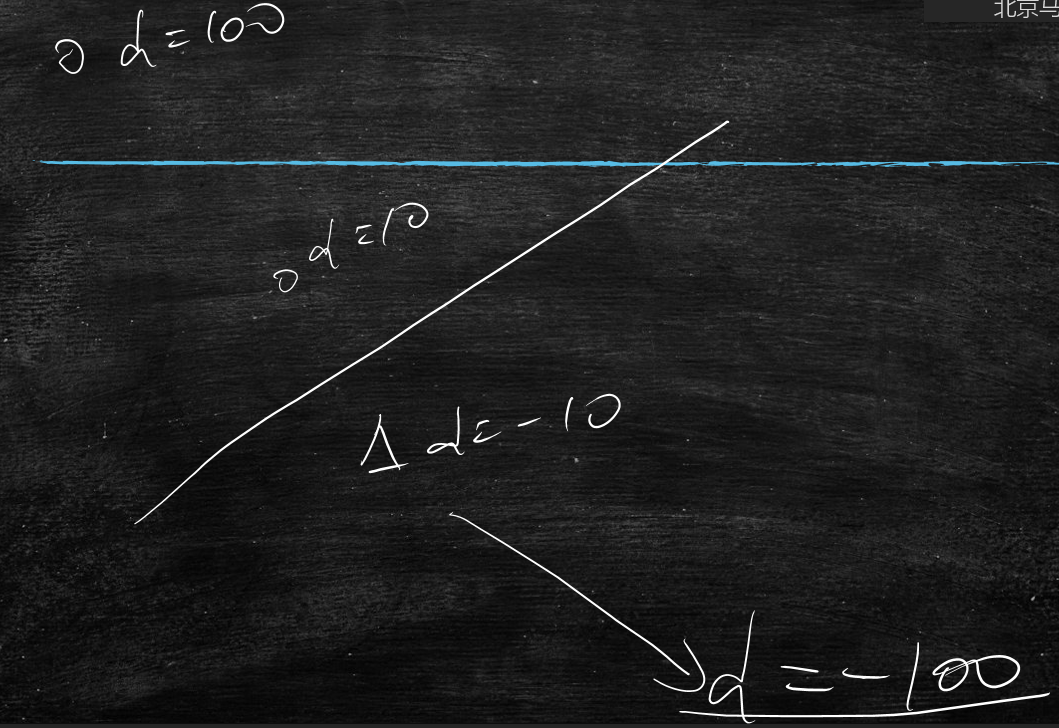
那么同样是d>0，d=10和d=100这两个有什么区别呢？
离直线越远d的数值越大，其实就是点到直线的距离
当点离着直线越近d=0，概率f越趋近于0.5
当点在直线上方，而且特别远时，概率f越趋近于1
当点在直线下方，而且特别远时，概率f越趋近于0
初始时，还是与线性回归一样，初始化随机一个w
x代表所有数据样本
x1代表样本第一条数据
f1代表x1代入模型后计算出的值
y1是真实的数值(0或1)
那么f1与y1是有差异，期望f1与y1的差异越小越好
是不是和mse很像呢
通过差异越小来不断调整w，让f与y不断的接近，所以这里还是线性回归的思想
在线性回归里，我们定义的mse为：
$$
mse=\frac{1}{n}\sum_{i=1}^{n}({f_i}-{y_i})^2
$$
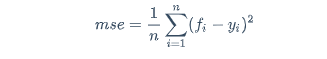
不断的找w，让mse最小
那么在逻辑回归中还可以使用mse吗？
答：不能，为什么不能，后续会讲解
那么既然这种mse不行，咱们要找出一种可以的
找一种新的距离，来度量预测值和真实值
预测值是个概率，比如发生的概率是0.9，不发生的概率是0.1
对应的真实是1和0
其实就是两个概率之间的距离，求解概率距离，引申出KL距离
KL距离
p和q是两个概率分布
xi是样本情况
n是概率分布的总情况
$$
KL=\sum_{i=1}^{n}p(x_i) \cdot log\frac{p(x_i)}{q(x_i)}
$$
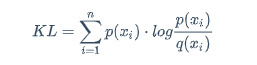
上面直接上公式，估计大部分人会蒙
下面通过例子讲解
比如有两枚不均匀的硬币(p和q)，
p抛正面的概率为1/3
p抛反面的概率为2/3
q抛正面的概率为1/4
q抛反面的概率为3/4
求解一下这两枚的差异有多大？
代入KL公式
$$
KL=\sum_{i=1}^{n}p(x_i) \cdot log\frac{p(x_i)}{q(x_i)}
$$
由于抛硬币只有正面和反面，所以n=2
正面情况：
$$
\frac{1}{3} \cdot log\frac{\frac{1}{3}}{\frac{1}{4}}
$$
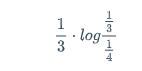
反面情况：
$$
\frac{2}{3} \cdot log\frac{\frac{2}{3}}{\frac{3}{4}}
$$
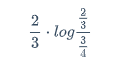
然后正与反求和，算出距离就是差异
极端情况，两个硬币一样材质，那么距离就是0
KL距离公式，具备距离的性质，但是又不具有距离的性质
比如欧式距离，从A点到B点是等于从B点到A点距离的，具有对称性
而KL距离，不具备对称性
概率p到概率q的距离不等于概率q到概率p的距离
$$
\sum_{i=1}^{n}p(x_i) \cdot log\frac{p(x_i)}{q(x_i)}\neq\sum_{i=1}^{n}q(x_i) \cdot log\frac{q(x_i)}{p(x_i)}
$$
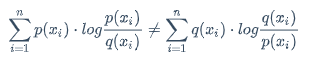
当x不是离散值，取的是连续值时，公式改进为将累加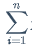号
变成积分号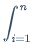
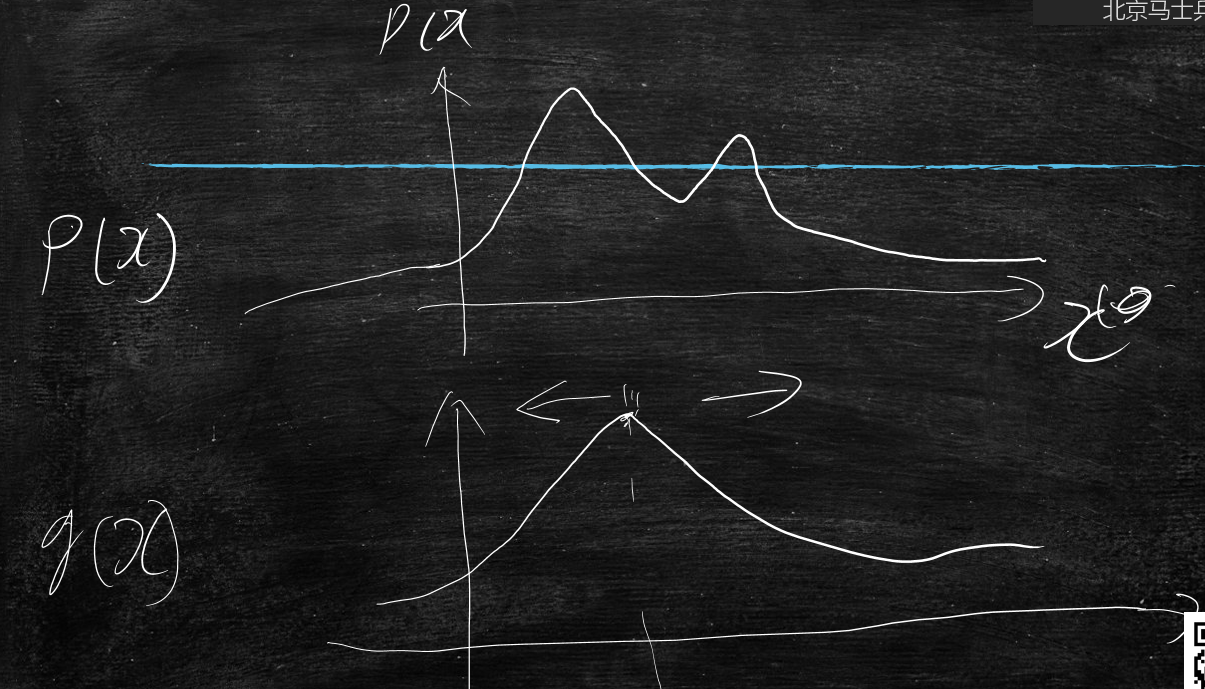
比如p(x)是个概率分布，它大概图形如下图所示，有两个山峰
曲线到x轴的面积是1
q(x)是个概率分布，它大概图形如下图所示，有一个山峰，它的峰顶可以自由的向左右移动
q1(x)的峰顶点移动到了p(x)第一个山峰的峰顶点了
q1(x)的峰顶点移动到了p(x)第一个山谷的谷底点了
那么p(x)到q1(x)的距离KL(p,q1)与p(x)到q2(x)的距离KL(p,q2)哪个距离小？
分析一下：
将公式简化一下：
$$
\sum_{i=1}^{n}p(x_i) \cdot log\frac{p(x_i)}{q(x_i)}\rightarrow\sum_{i=1}^{n}p(x_i) \cdot log , p(x_i)-p(x_i) \cdot log , q(x_i)
$$
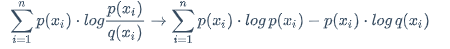
接下来先看第一部分：
$$
p(x_i) \cdot log , p(x_i)
$$
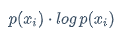
这个部分与q无关，所以这部分是个常数
由于第一部分是常数，那么让整体变小，就是要让第二部分变大
再看第二部分：
$$
p(x_i) \cdot log , q(x_i)
$$
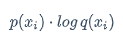
要牢记p是概率范围是(0~1)
当p大时，q越大越好
当p趋近于0时，q无所谓了
所以回到问题：p(x)到q1(x)的距离KL(p,q1)与p(x)到q2(x)的距离KL(p,q2)哪个距离小？
答：p(x)到q1(x)的距离KL(p,q1)距离小，因为当p最大的时候，q1最大
那么把距离反过来，q1(x)到p(x)的距离KL(q1,p)与q2(x)到p(x)的距离KL(q2,p)哪个距离小？
答：
$$
\sum_{i=1}^{n}q(x_i) \cdot log\frac{q(x_i)}{p(x_i)}\rightarrow\sum_{i=1}^{n}q(x_i) \cdot log , q(x_i)-q(x_i) \cdot log , p(x_i)
$$
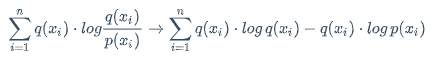
先看第一部分：
$$
q(x_i) \cdot log , q(x_i)
$$
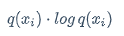
这个部分与p无关，所以这部分是个常数
由于第一部分是常数，那么让整体变小，就是要让第二部分变大
再看第二部分：
$$
q(x_i) \cdot log , p(x_i)
$$
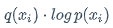
分析下对数曲线：
当p=1时，logp=0
当p->0时，logp将很快趋近于负无穷
当p->正无穷时，logp会变的平缓
由于p和q是概率，范围只能在0~1之间
那么logp就是小于0的值
当p变小时，logp很快趋近于负无穷
所以只有q变小时，才可能消除logp带来负无穷的影响
比如说logp=-10000，那么q=0.9，qlogp=-9000
那么q=0.1，qlogp=-1000
所以当q变小时，qlogp变大
结论：
当计算KL(p,q)的时候，q尽可能匹配p的大值
当计算KL(q,p)的时候，q尽可能匹配p的小值
再回到KL距离
发生概率f=0.9，真实值是y=1
若是距离是：ylogy/f，这个会有什么问题？
当y=1时，f->1
当y=0时，f随意
这样y=0的情况就学习不到
计算距离要将不发生概率加进来
$$
y \cdot log , \frac{y}{f} + (1-y) \cdot log , \frac{1-y}{1-f}
$$
这种概率上的差异应该叫交叉熵损失
$$
\sum_{i=1}^{n}[y_i \cdot log\frac{y_i}{f_i}+(1-y_i) \cdot log\frac{(1-y_i)}{(1-f_i)}]
$$
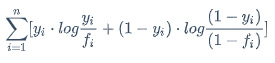
这两部分总有一部分为0
把它简化
$$
-\sum_{i=1}^{n}[y_i \cdot logf_i + (1-y_i) \cdot log(1-f_i)]
$$
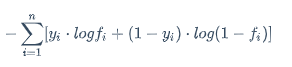
不用担心f=0导致log0->无穷的问题，因为f不可能等于0的，只会趋近于0
得出KL距离公式后：就不断改变w，让这个距离(KPI)最小，学习训练的过程
先随机出一个
w计算模型输出计算模型输出和真实数值的差异 得到损失函数（
mse，KL距离）不停地调整
w让损失函数变小