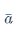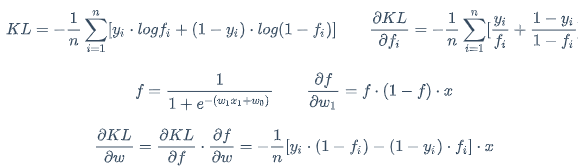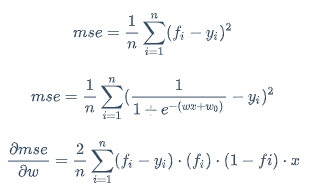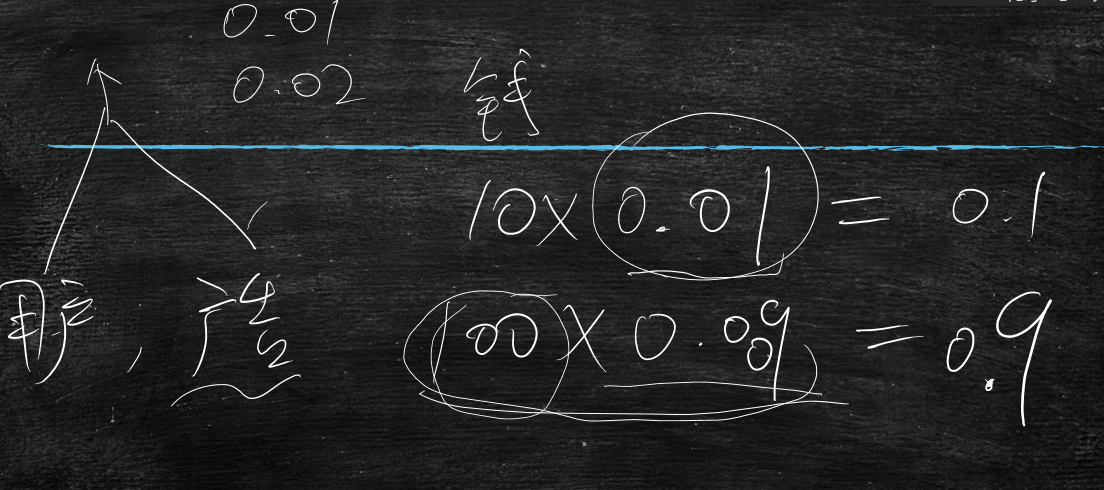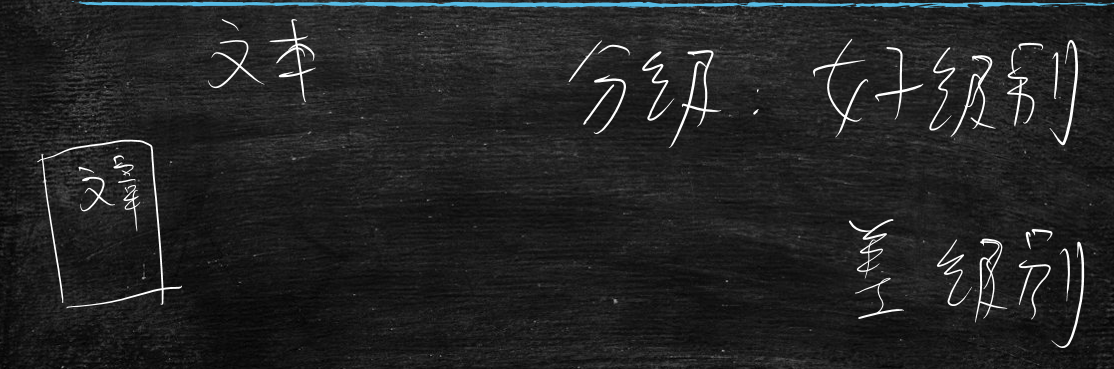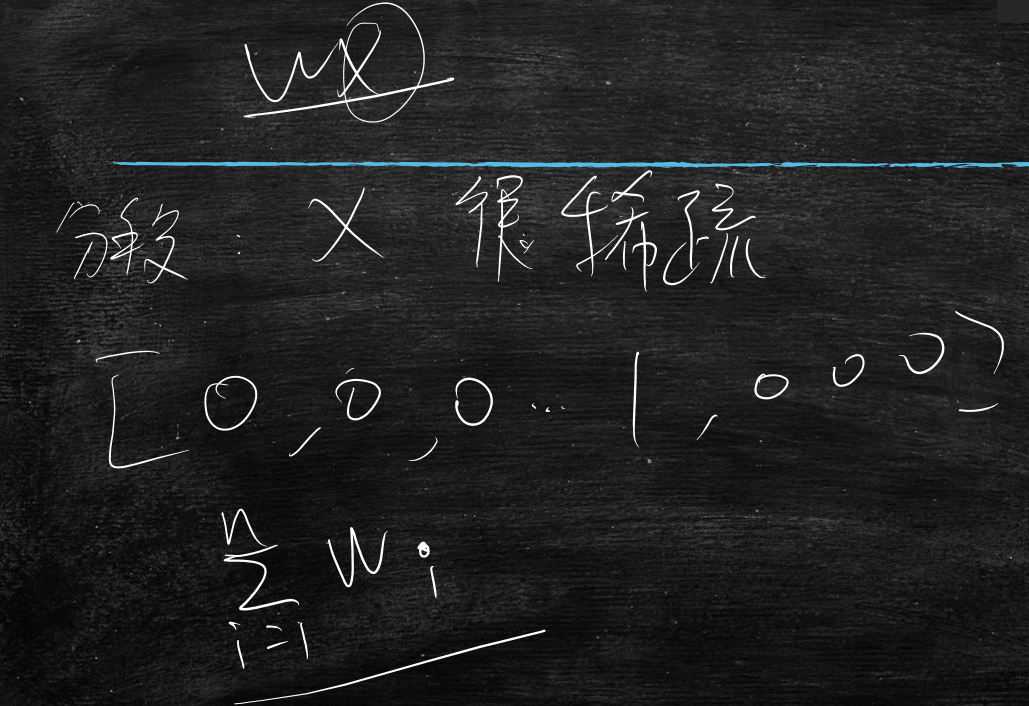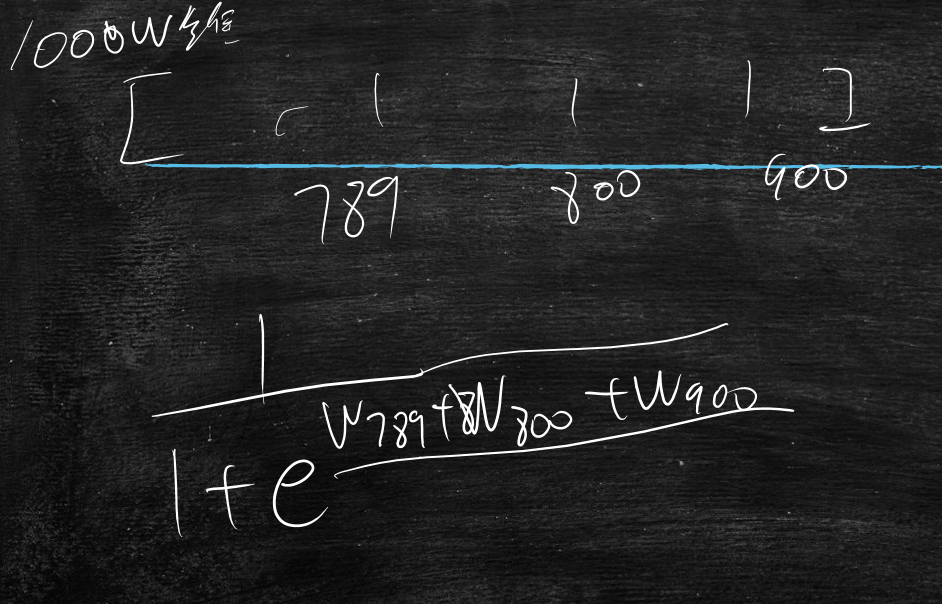ShiYu

# 损失函数推到解析和特征选择优化

逻辑回归-二分类

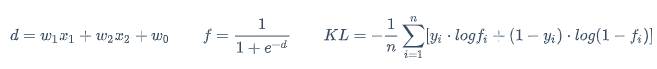
公式 $$ d=w_1x_1+w_2x_2+w_0 \qquad f=\frac{1}{1+e^{-d}} \qquad KL=-\frac{1}{n}\sum_{i=1}^{n}[y_i \cdot logf_i + (1-y_i) \cdot log(1-f_i)] $$ image-20220311140019874

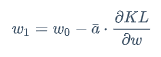
梯度下降学习w $$ w_1=w_0- \bar{a} \cdot \frac{\partial KL}{\partial w} $$ image-20220311140034652

其中image-20220311135908011为步长，学习因子

求导公式 $$ KL=-\frac{1}{n}\sum_{i=1}^{n}[y_i \cdot logf_i + (1-y_i) \cdot log(1-f_i)] \qquad \frac{\partial KL}{\partial f_i}=-\frac{1}{n}\sum_{i=1}^{n}[\frac{y_i}{f_i}+\frac{1-y_i}{1-f_i}] $$

$$ f=\frac{1}{1+e^{-(w_1x_1+w_0)}} \qquad \frac{\partial f}{\partial w_1}=f \cdot (1-f) \cdot x $$

$$ \frac{\partial KL}{\partial w}=\frac{\partial KL}{\partial f} \cdot \frac{\partial f}{\partial w}=-\frac{1}{n}[y_i \cdot (1-f_i)-(1-y_i) \cdot f_i] \cdot x $$

image-20220311141405020

image-20220311141348500

之前谈论过为什么不使用mse来计算逻辑回归的误差？

答：mse的导数不好用

推理mse的导数 $$ mse=\frac{1}{n}\sum_{i=1}^{n}(f_i-y_i)^2 $$

$$ mse=\frac{1}{n}\sum_{i=1}^{n}(\frac{1}{1+e^{-(wx+w_0)}}-y_i)^2 $$

$$ \frac{\partial mse}{\partial w}=\frac{2}{n}\sum_{i=1}^{n}(f_i-y_i) \cdot (f_i) \cdot (1-fi) \cdot x $$

image-20220311142337126

image-20220311142411480

那么mse导数的缺点：

  • 当随机初始化w非常大的数时，f要么趋近1，要么趋近0

  • 那么由于上点的特性，导致(fi)(1-fi)总会有一项趋近为0，导致整个导数变的非常小

  • 梯度下降法中，那么就会影响w的学习速度，导致w根本不会发生更改，学不到了

    image-20220311143148665

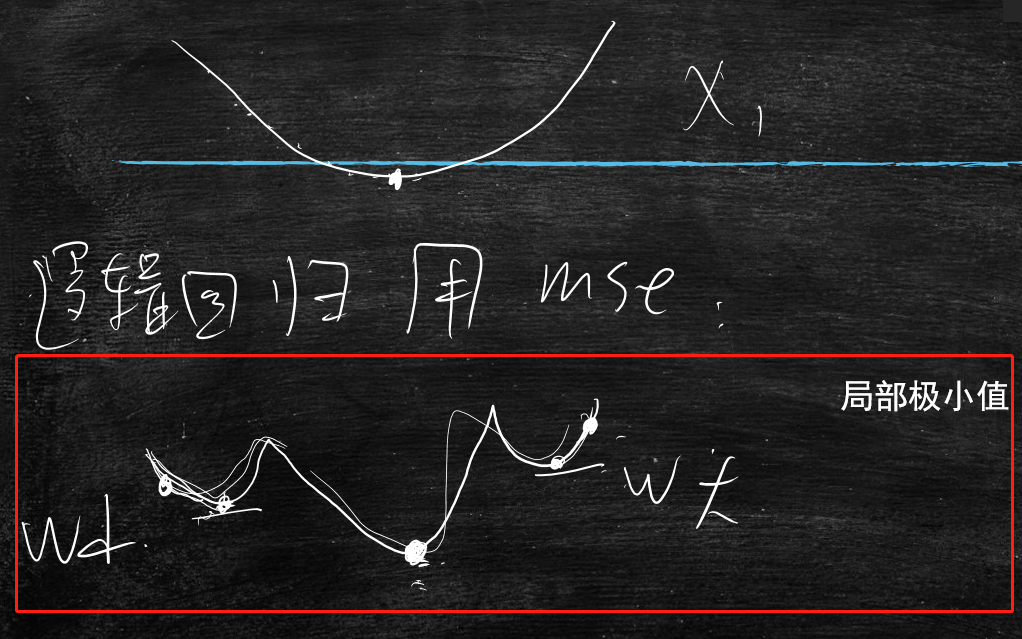
  • 使用mse时，会产生局部极小值，因为w对mse的曲线如下图红框所示

    image-20220311143344895

  • 而使用KL时，不会产生局部极小值，大致曲线是凸函数

    image-20220311143457479

在机器学习的前沿领域，很多研究都是在研究怎么选取初始点，但是在工程上达不到很好的效果

因为w对mse的曲线的局部极小的数量 和 维度的平方成正比，也就是说100维的，就会产生10000的局部极小

image-20220311144010803

所以不使用mse，而使用KL距离

代码例子

train.py

# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_predict
from numpy import shape
from sklearn import metrics
from sklearn.metrics import log_loss
import numpy as np
def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=np.array(X)
	y=np.array(y)
	return X,y
def curve(x_train,w,w0):
	results=x_train.tolist()
	for i in range(0,100):
		x1=1.0*i/10
		x2=-1*(w[0]*x1+w0)/w[1]
		results.append([x1,x2])
	results=["{},{}".format(x1,x2) for [x1,x2] in results]
	return results	
	

X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
 
 
model = LogisticRegression()
model.fit(X_train, y_train)
 
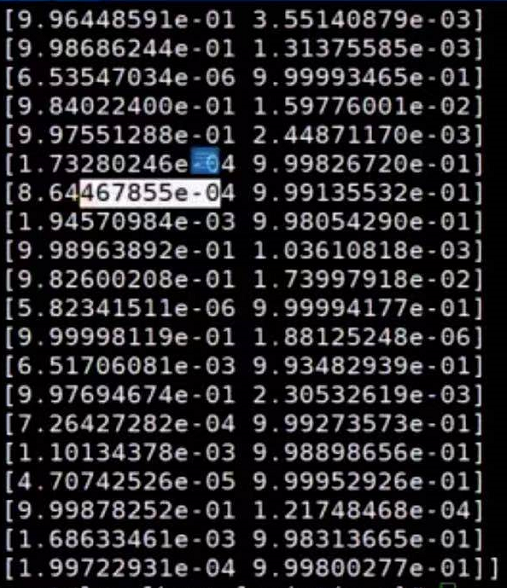
print "w",model.coef_
print "w0",model.intercept_

#y_pred = model.predict(X_test)
#print y_pred
y_pred=model.predict_proba(X_test)  # 输出概率形式的
print y_pred
#loss=log_loss(y_test,y_pred)
#print "KL_loss:",loss
#loss=log_loss(y_pred,y_test)
#print "KL_loss:",loss
'''
curve_results=curve(X_train,model.coef_.tolist()[0],model.intercept_.tolist()[0])
with open("train_with_splitline","w") as f :
	f.writelines("\n".join(curve_results))
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

执行结果

image-20220311150159075

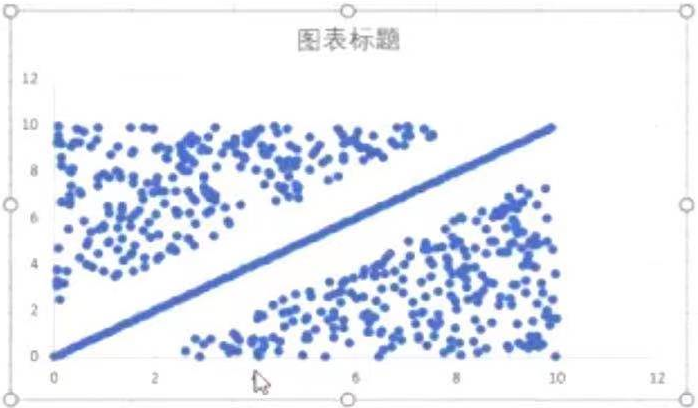
逻辑回归学习的结果

image-20220311145348483

画一条直线能把，这两部分分开，能画出多少条直线呢？答：无数条，但是学习到的那条直线一般在空白的中间处

逻辑回归中概率形式比分类形式有什么好处呢？

  • 可排序

    比如：用户还有广告来预测点击，一般点击的概率都不会太高，但是可以从矮子中选高的，找到一个最高的，推送给用户；

    一般投广告要给搜索引擎投钱，

    比如投了10元钱，模型预测的点击率为0.01，那么收益率为0.1

    投了100元钱，模型预测的点击率为0.009，那么收益率为0.9

    说明了虽然下面的点击率低，但是收益率却比第一种高

    所以要投广告，一个是内容好，一个是烧钱，也说明只要模型预测的点击率稍微准一点点，那么就能盈利

    因为广告是按点击收费的

    image-20220311150634341

  • 比如做个内容分发网站、门类网站，很多用户会在网站上发布内容，如文章，那么网站要对文章进行分级：

    分为好的级别分发就大一些流量也大一些，差级别的可能就不分发了

    这时就能使用机器学习，将好的文章标识为1，差的文章标识为0，在使用逻辑回归模型预测分数(0~1)

    一般来说0.9以上的交给人工确认看是否真的好，0.1一下的也交给人工确认看是否真的差

    那么0.1~0.9的不用管，作为普通数据处理即可，这样就能把100w的文章一下子降到几千的量级，几千的话人工就能看过来了

    image-20220311152134728

    image-20220311152154422

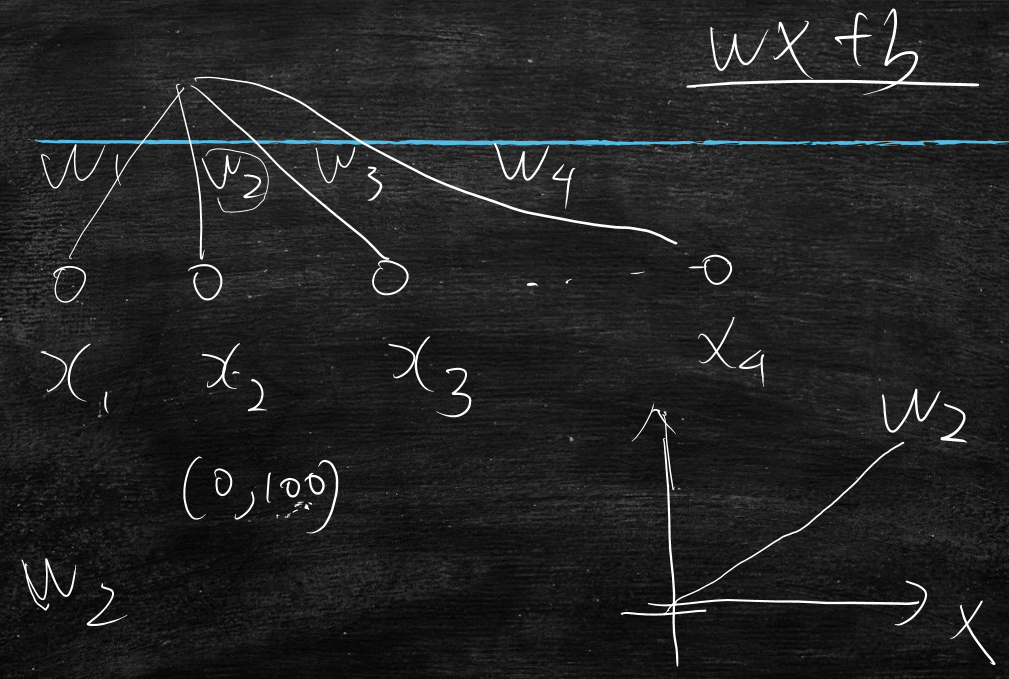
多分类如何实现？

比如有n个分类，x输入模型，输出n+1类结果

为什么是n+1类呢？还有一类是不属于n个分类的分类

但是在企业中，你的分类体系会经常的变动，调整，比如今天是10个分类，明天又说5个分类就行，后天又让改到11个分类，所以这里要来回的修改

所以为了应对频繁的更改，将n分类问题，转化为n个二分类问题

将x1交给第一分类的模型，输出第一分类的概率值f1

将x2交给第一分类的模型，输出第一分类的概率值f2

将x3交给第一分类的模型，输出第一分类的概率值f3

。。。

将xn交给第一分类的模型，输出第一分类的概率值fn

然后比较所有f，哪个f大则是哪个分类，若是都不大则属于n+1分类(什么也不是的分类)

这样即便要加分类，单独训练要加的分类即可

要是减分类，则去掉那个分类就行，这样特别灵活

这是个纯工程的思维即开闭原则

image-20220311160532771

逻辑回归的那些缺点及不足

比如下图所示的二分类问题：如何画线将圆圈与三角形分开呢？

这是个异或问题

这种叫做线性不可分，就是用直线是不能分开的

那么在真实场景中是线性可分的场景多还是不可分的场景多呢？

答：大量的是不可分的场景多

image-20220311160729191

尝试找到解决线性不可分的问题的方法

二维平面里面解决不了，可以到三维立体中看看，

可以将二维变为三维

比如原始坐标为(x1,x2)，变为(x1,x2,x1x2)

将(1,1)变为(1,1,1)

将(0,0)变为(0,0,0)

将(1,0)变为(1,0,0)

将(0,1)变为(0,1,0)

这时候抬高(1,1,1)变为(1,1,3)

image-20220311162355484

image-20220311162657270

这时就能用切面将其分开来，然后此切面投射在底面的双曲线就是分隔曲线

代码示例

train_noseparability.py

# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_predict
from numpy import shape
from sklearn import metrics
import numpy as np
import random
def curve(x_train,w,w0):
	results=x_train.tolist()
	results=[x[0:2] for x in results]
	step=0.0001
	for i in np.arange(-0.2,1.2,step):
		x1=i+step
		x2=-1*(w[0]*x1+w0)/(w[1]+w[2]*x1)
		if abs(x2)>5.0:
			continue
		results.append([x1,x2])
	results=["{},{}".format(x1,x2) for [x1,x2] in results]
	return results	
def get_data(center_label,num=100):
	X_train=[]
	y_train=[]
	sigma=0.01
	for point,label in center_label:
		c1,c2=point
		for _ in range(0,num):
			x1=c1+random.uniform(-sigma,sigma)
			x2=c2+random.uniform(-sigma,sigma)
			X_train.append([x1,x2])
			y_train.append([label])
	return X_train,y_train
		
center_label=[[[0,0],1],[[1,1],1],[[0,1],0],[[1,0],0]]
X_train,y_train=get_data(center_label)
#X_train=10*[[0,0],[1,1],[1,0],[0,1]]
# 让第一维乘以第二维作为第三维
X_train=[ x+[x[0]*x[1]] for x in X_train]
X_train=np.array(X_train)
 
#model = LogisticRegression(penalty="l2")
model = LogisticRegression()
model.fit(X_train, y_train)
 
print (model.coef_)
print (model.intercept_)
curve_results=curve(X_train,model.coef_.tolist()[0],model.intercept_.tolist()[0])

with open("no_separa_traindata.csv","w") as f :
	f.writelines("\n".join(curve_results[0:400]))
with open("no_separa_train_with_splitline.csv","w") as f :
	f.writelines("\n".join(curve_results))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

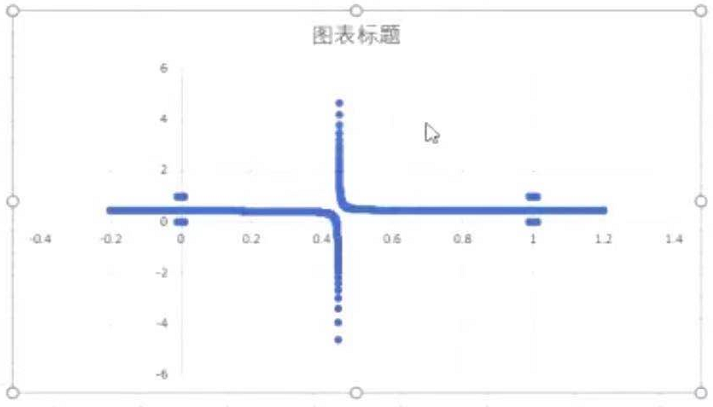
将(1,1)，(0,0)，(1,0)，(0,1)这四个中心点分布一些点，如下图所示：

image-20220311163154957

在增加一维，让第一维乘以第二维作为第三维

原始点分布

image-20220311164016500

训练后双曲线分隔

image-20220311164049076

所以可以通过特征组合，不断改变w，将一条直线变为各种稀奇古怪的曲线

利用简单的模型，通过在特征上各种组合，解决复杂问题时也能达到比较好的效果

image-20220311164502381

再举个例子

比如电商平台，预测用户购买商品，利用用户画像及商品

其中用户中有个维度是年龄x1(1维好还是分段好?)

商品x2

定义逻辑回归模型然后输出y购买的概率值

image-20220311165219982

若是年龄用一维，那么年龄维度的x2对于wx+b整个的贡献是线性的，并且该直线的斜率是w2

image-20220311165234894

若是年龄是分段的，分为两段[0~50]，[50~100]，那么年龄维度的x2对于wx+b整个的贡献是折线

这样表达能力更强了

image-20220311165250790

分段还有什么好处呢？

比如在真实工程中，都要算逻辑回归模型的，大量要算下图所示的公式

工程上x的维度会非常高，上万维，但是若是在线服务的话可能QBS要几万次

那么数据量及计算量非常大

image-20220311165303358

若进行分段会让x很稀疏，就是大量为0，偶尔出现1

那么当计算时，只要x是1的计算即可

这样虽然维度很多，但是大量为0，不用参与运算，计算速度提升

image-20220311165315566

或者x就搞成是0，1；那么公式就变为w的累加

这样连乘法都没有了，只有加法了

image-20220311171326060

再看一个多元的回归例子

通过身体指标，预测未来患有癌症的概率

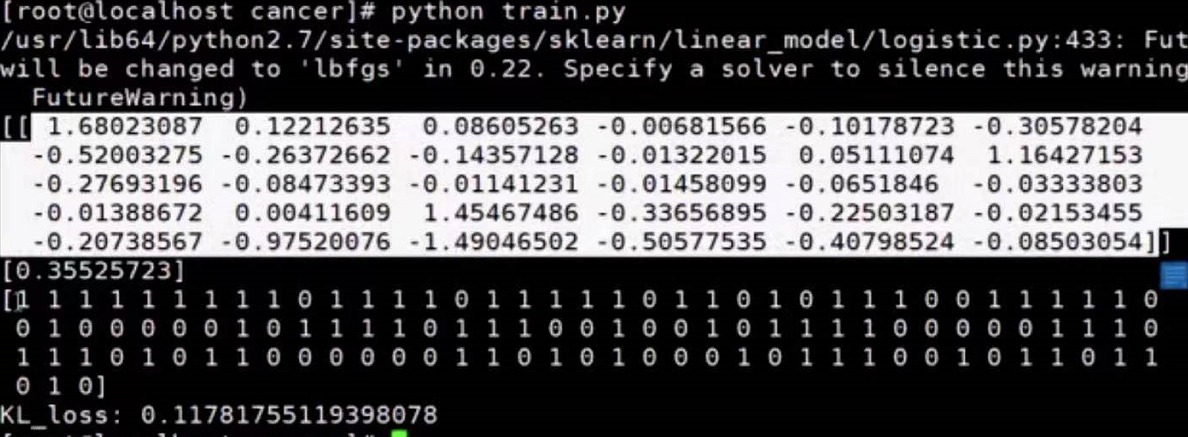
train.py

# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_predict
from numpy import shape
from sklearn import metrics
from sklearn.metrics import log_loss
import numpy as np
def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
 
 
model = LogisticRegression()
model.fit(X_train, y_train)
 
print (model.coef_)
print (model.intercept_)
 
y_pred = model.predict(X_test)
y_pred=model.predict_proba(X_test)
print y_pred
loss=log_loss(y_test,y_pred)
print "KL_loss:",loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

执行结果

image-20220311171902942

根据身体指标x，通过模型，输出y

若是y>0.5，则是

若是y<0.5，则否

觉得这样合理吗？

在实际工作中，阈值不会卡在0.5

因为如果一个人他没有得癌症，但是预测他得了，最多让他复查一下就行了

但是如果他得癌症了，但是预测他没有得，那就麻烦了

image-20220311172059535

因为分类器包括所有模型都有一定的错误率

这里的错误率是

当他是1时，y<0.5

当他是0时，y>0.5

解决办法是为了不漏，降低些权重，

如：卡到0.2或0.1

用以保证是癌症的人能找出来

image-20220311172444897

数据倾斜问题

逻辑回归模型训练过程中，怎么训练这个w

训练这个w的过程就是画直线的过程

那么单独看一个点，这个点是希望直线离自己越远越好，就是让f趋近于1

所以从这个点来看，训练过程就是点把这个直线往下推

image-20220311173319766

那么问题来了，上面的点把直线往下推，下面的点把直线往上推，直至推不动时，就是训练出来的w

image-20220311173333431

假如，在圆形点有9999个样本，但是三角形点有1个样本，会出现什么情况？

答：圆形点可能把直线推过于三角形点的位置，就是比三角形点的位置还下面

image-20220311173348759

解决方案就是样本均衡

  • 下采样：将多样本，下降其样本数量
  • 上采样：将少样本，重复复制其样本

image-20220311173826530

比如，广告真实数据肯定是0的非常多就是点击的人多，这时就要重复复制1的数据

image-20220311173846367

← 到底好不好？模型评价指标讲解 →