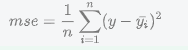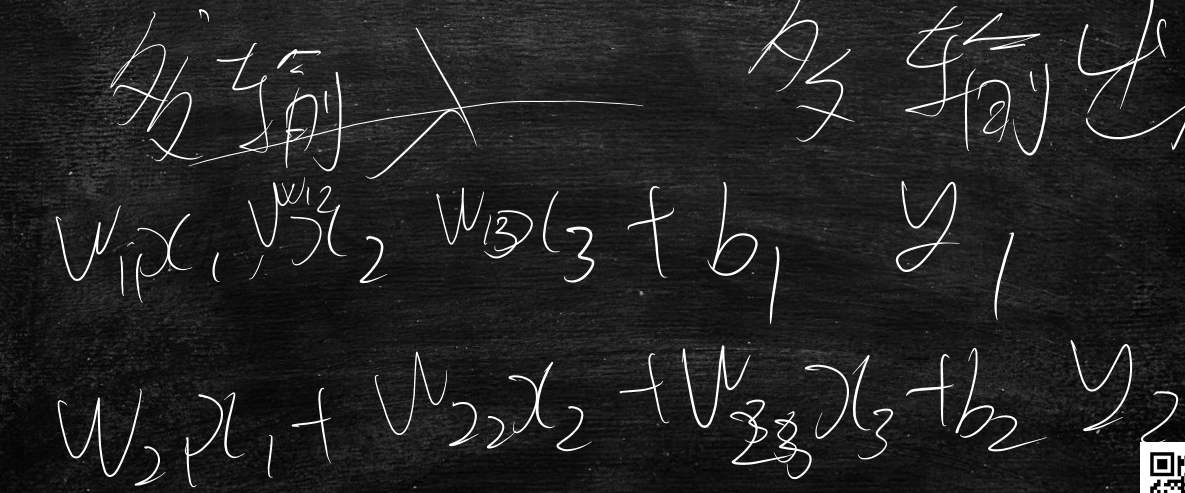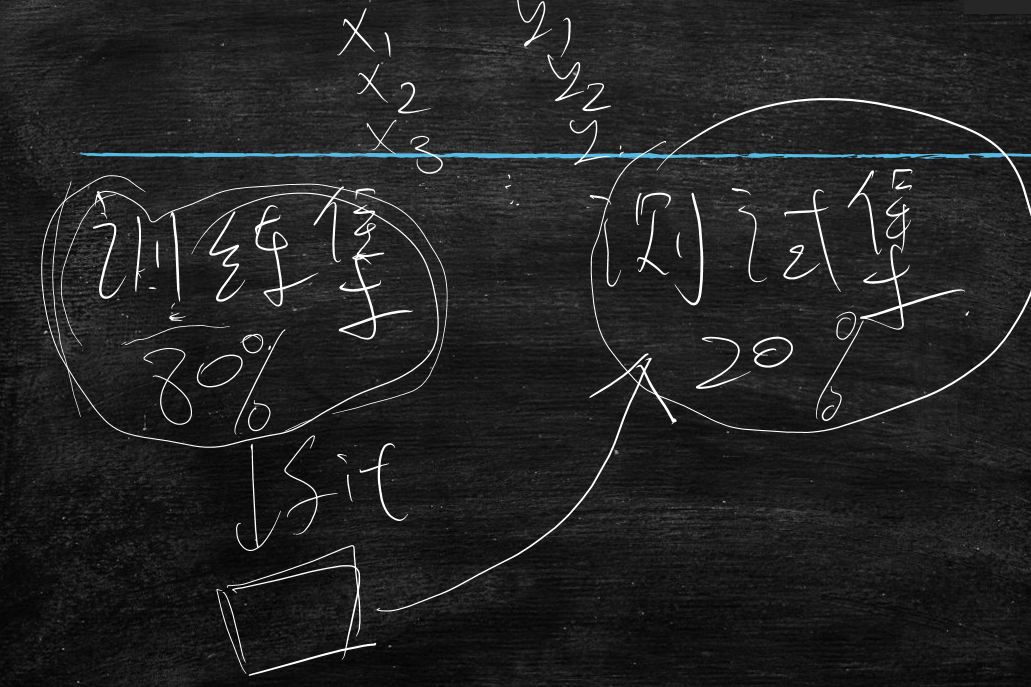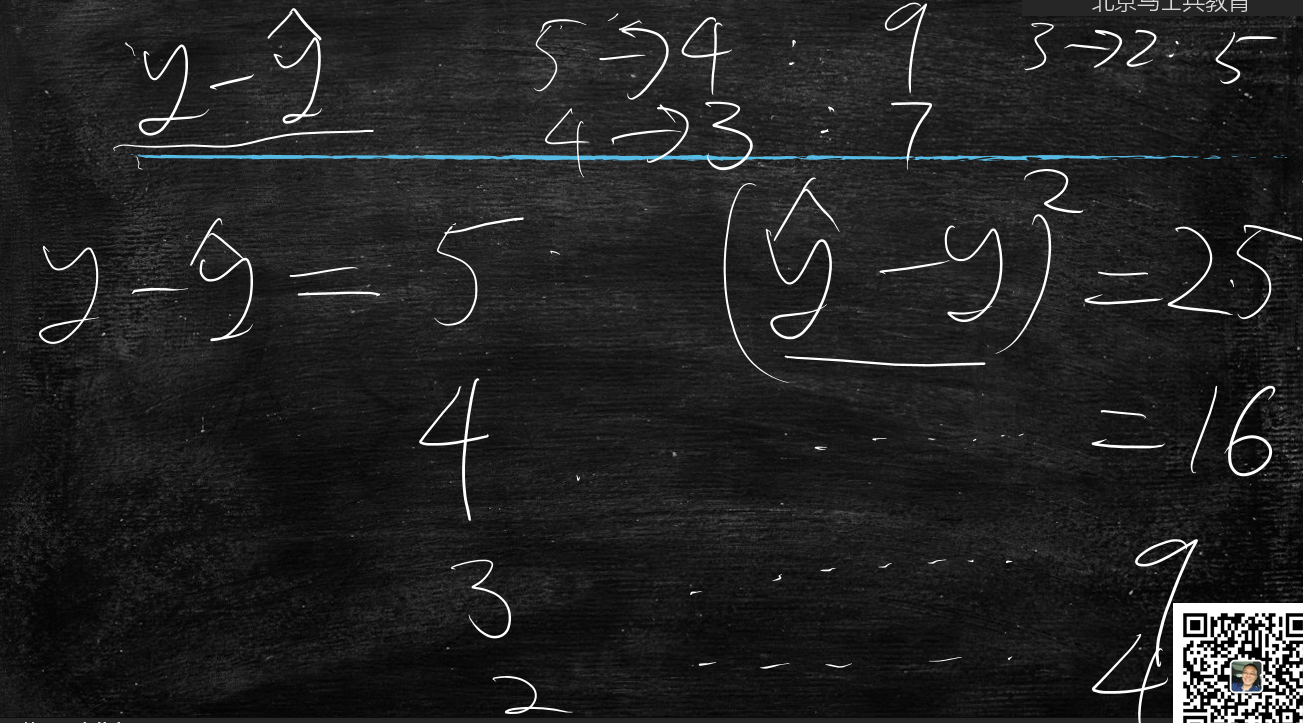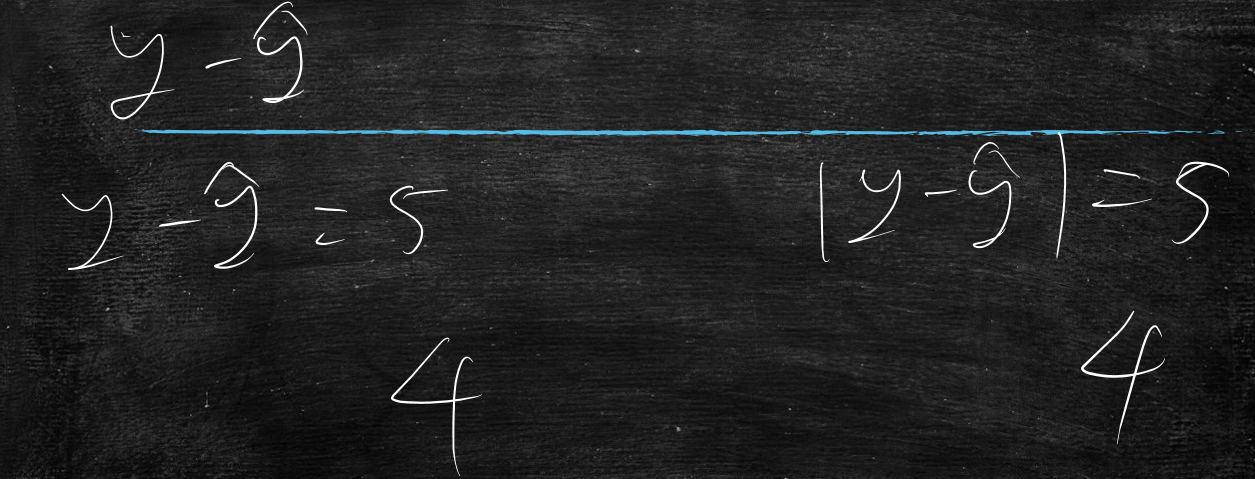# 第一个模型用来进行数值预测
AI大致过程
特征提取(向量化)
通过网页、图像、用户画像等数据根据业务规则、属性划分向量,这步就是向量化,这是AI、机器学习的基石,一般要与业务强绑定,和产品经理沟通出来的
学习过程
上一步中得到向量,交与模型进行学习,最后得到输出结果
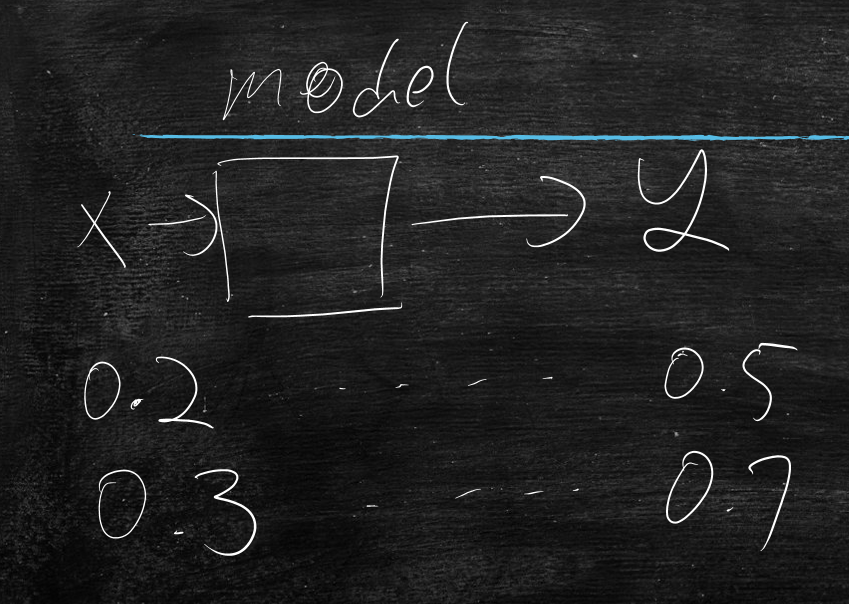
今天就进行模型中的最简单的模型,线性回归
线性回归
训练数据:一堆[[x],[y]]
模型:y=wx+b
在坐标系中体现:就是一条直线,w越大直线越斜,b是在y轴的偏移,由于是一条直线所以是线性回归
回归:拟合、模拟,将w、b猜出来就是回归
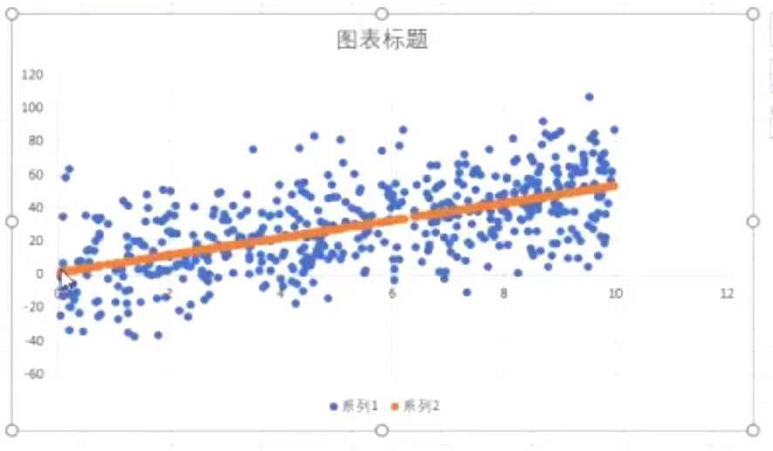
一堆x、y在图表长什么样子?
那么,线性回归想做的事情就是,通过已知的x、y的分布,找出这么一条直线尽可能多的穿过这些点,不断的调整w和b,让这条直线尽可能的拟合这些x、y。
简单推导线性回归的实现逻辑
假设就一个点,那么就有无数个w,b;无数解,没有唯一解
假设两个点,那么就只有一条直线,唯一解
结论:点少时,不需要机器学习;
那么当三个点时,而且第三个点并不在另外两点的连线上,那么问题来了:就至少有一点产生误差
不断的调整w和b,找到合适的w、b,让一条直线穿过更多的点(训练数据),更加拟合训练数据,让误差变小
引申出MSE(均方误差:Mean(均值) Squared(平方) Error(误差))
$$ mse=\frac{1}{n}\sum_{i=1}^{n}(y-\bar{y_i})^2 $$
问题:误差计算中绝对值算法好还是方差算法好呢?
答:平方好,方差更能体现收益
那么线性回归问题就转化为了不断的调整w和b,让MSE最小。
就变为了求最小值,那么求最小值有两种方法:
- 有解析解
- 无解析解:其中机器学习主要针对无解析解来计算
AI不仅仅是Python实现,也可以用Java、C来实现,只不过Python的AI生态好,有许多方便的AI学习算法包等,下面是Python调用线性回归模型例子:
train.py
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import metrics
def curce_data(x,y,y_pred):
x=x.tolist()
y=y.tolist()
y_pred=y_pred.tolist()
results=zip(x,y,y_pred)
results=["{},{},{}".format(s[0][0],s[1][0],s[2][0]) for s in results ]
return results
def read_data(path):
with open(path) as f :
lines=f.readlines()
lines=[eval(line.strip()) for line in lines]
X,y=zip(*lines)
X=np.array(X)
y=np.array(y)
return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
#一个对象,它代表的线性回归模型,它的成员变量,就已经有了w,b. 刚生成w和b的时候 是随机的
model = LinearRegression()
#一调用这个函数,就会不停地找合适的w和b 直到误差最小
model.fit(X_train, y_train)
#打印W
print model.coef_
#打印b
print model.intercept_
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
运行
python train.py
[[5.22515141]]
[1.36152602]
2
3
为什么W是多维的?b是一维的?
多输入,多输出的
机器学习中的一个重要概念
测试集和训练集
一般训练集占80%,测试集占20%;在训练集上通过fit函数找到合适的W和b,在测试集上看效果(MSE的值)
代码
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import metrics
def curce_data(x,y,y_pred):
x=x.tolist()
y=y.tolist()
y_pred=y_pred.tolist()
results=zip(x,y,y_pred)
results=["{},{},{}".format(s[0][0],s[1][0],s[2][0]) for s in results ]
return results
def read_data(path):
with open(path) as f :
lines=f.readlines()
lines=[eval(line.strip()) for line in lines]
X,y=zip(*lines)
X=np.array(X)
y=np.array(y)
return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
#一个对象,它代表的线性回归模型,它的成员变量,就已经有了w,b. 刚生成w和b的时候 是随机的
model = LinearRegression()
#一调用这个函数,就会不停地找合适的w和b 直到误差最小
model.fit(X_train, y_train)
#打印W
print model.coef_
#打印b
print model.intercept_
#模型已经训练完毕,用模型看下在训练集的表现
y_pred_train = model.predict(X_train)
#sklearn 求解训练集的mse
# y_train 在训练集上 真实的y值
# y_pred_train 通过模型预测出来的y值
#计算 (y_train-y_pred_train)^2/n
train_mse=metrics.mean_squared_error(y_train, y_pred_train)
print "训练集MSE:", train_mse
#看下在测试集上的效果
y_pred_test = model.predict(X_test)
test_mse=metrics.mean_squared_error(y_test, y_pred_test)
print "测试集MSE:",test_mse
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
运行
python train.py
[[5.22515141]]
[1.36152602]
训练集MSE:419.6364995873529
测试集MSE:438.41156782915124
2
3
4
5
训练集的线性图表展示
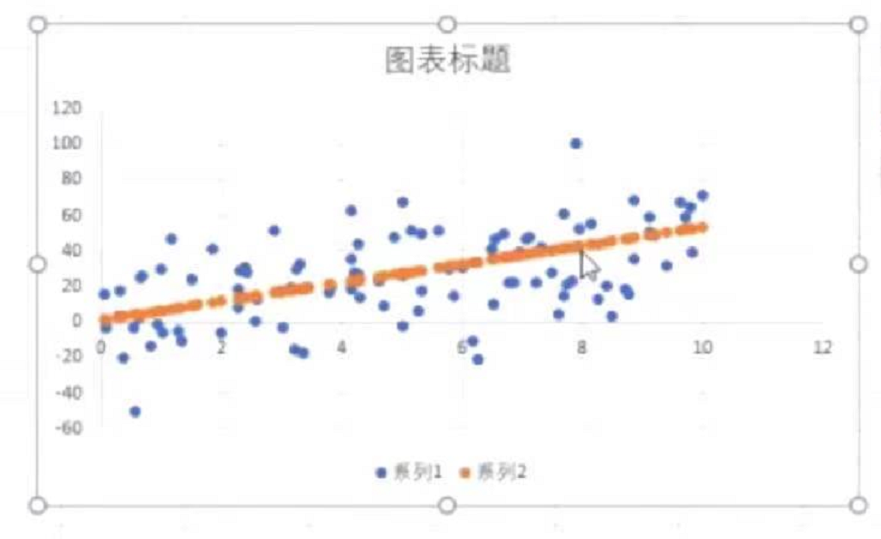
测试集的线性图表展示
达到的效果是在训练集上效果好,在测试集上效果也不差才行
机器学习与传统开发的区别
传统开发:从框架到理论
机器学习:从理论到框架
通过上述运行结果,得出训练集误差与测试集误差有什么区别?
测试集的误差一定大于训练集吗?不一定
data:全量数据
train_data:训练集
test_data:测试集
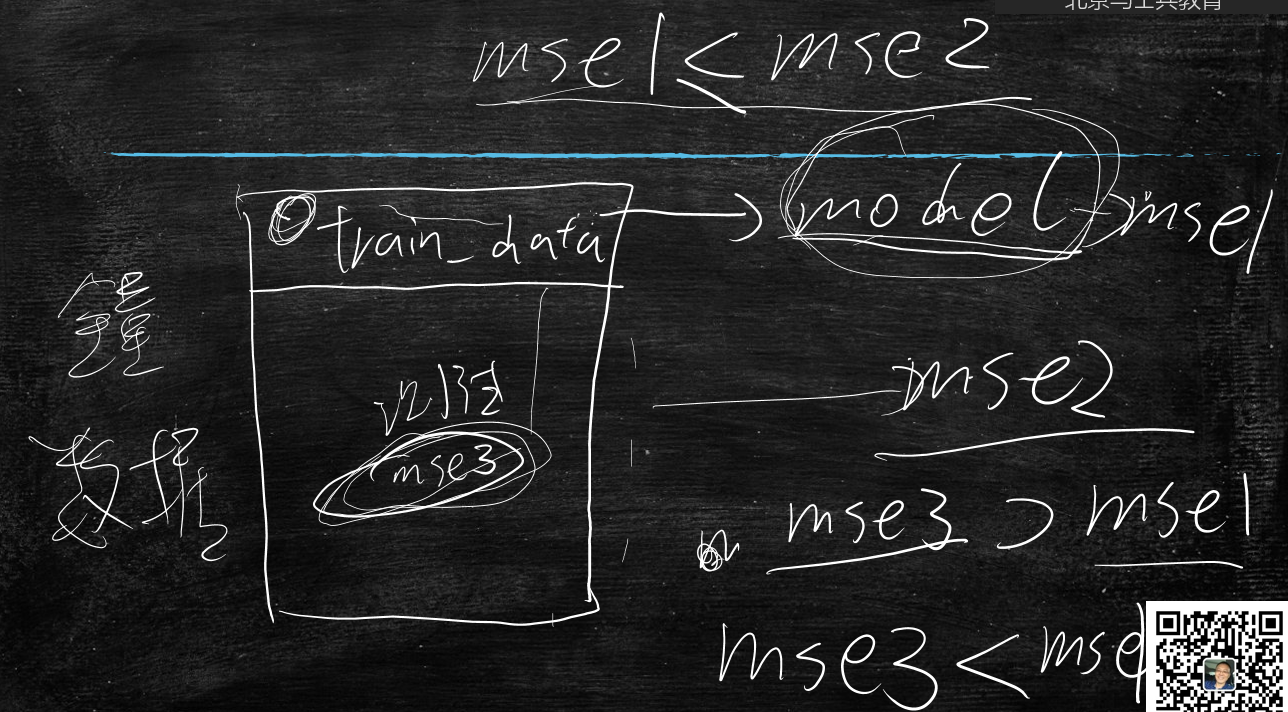
一般来说模型是通过训练集做的优化的,训练集通过model跑出mse1,全量数据通过model跑出mse2;mse1<=mse2
测试集通过model跑出mse3,若是采样中都是过训练集的点,则mse3<mse1(有可能);
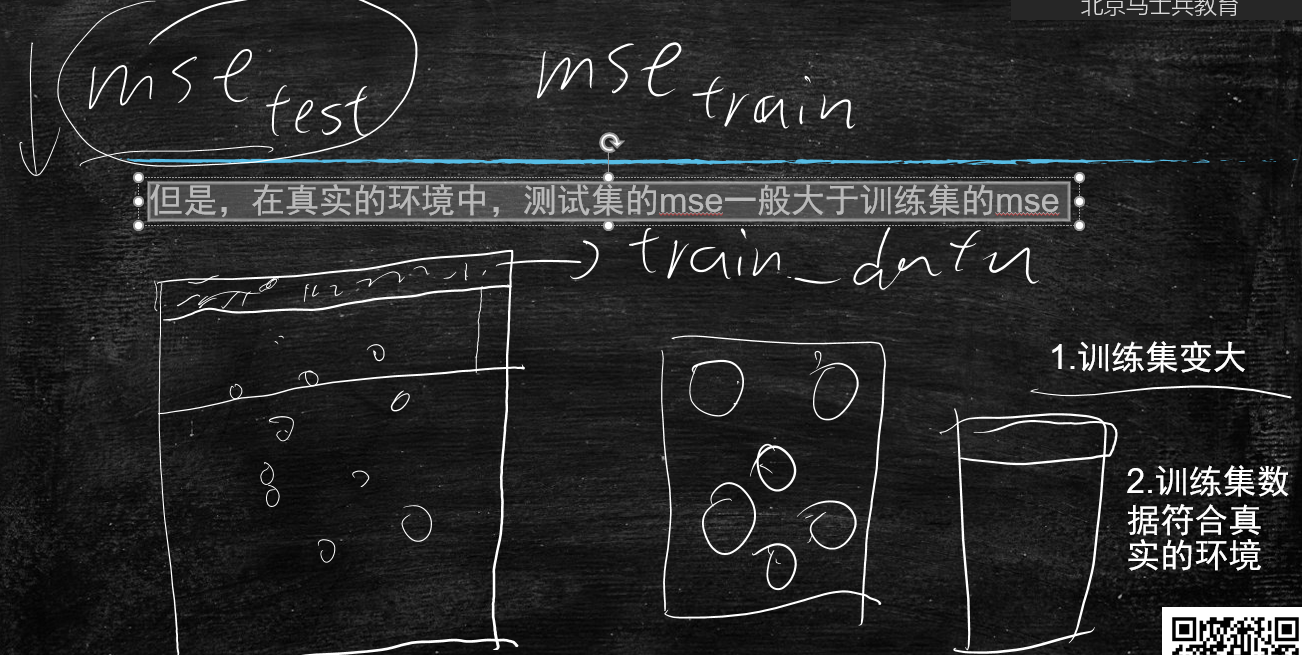
但是,在真实的环境中,测试集的mse3一般大于训练集的mse1
要想让测试集的效果好,有何办法?
- 训练集变大,这也是搞机器学习,要用大数据的原因
- 训练集数据符合真实的环境(多样性)
在拼多多上训练的模型,拿到京东上可以使用吗?
答:不行,因为各自的业务定位不同,所以每个公司都要搞自己的模型,不像架构,搞一套全能用,这种算法差异性很大。
**推广能力(泛化能力):**能在测试集上表现良好的能力
测试集的mse和训练集的mse谁大谁小
讲解疑问
为什么误差计算用方差不用绝对值?
方差能够体现收益
误差5时,方差25
误差4时,方差16 收益9
误差3时,方差9 收益7
误差2时,方差4 收益5
收益减少
绝对值
误差5时
误差4时 收益1
误差3时 收益1
误差2时 收益1
收益不变
结论
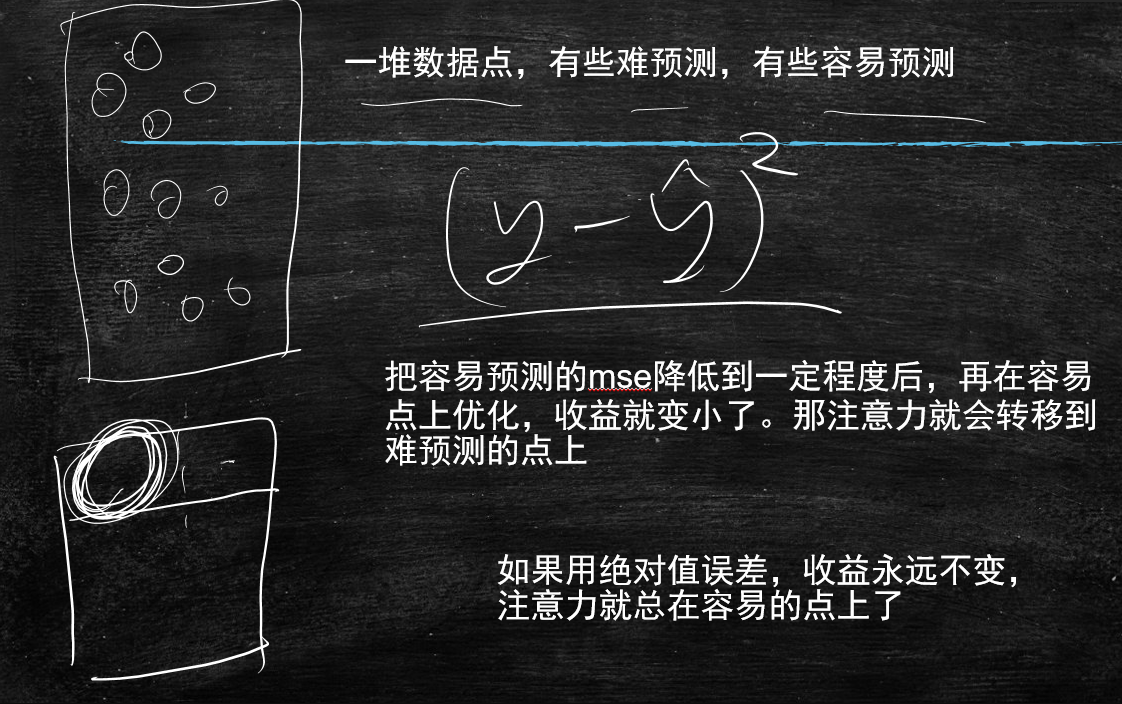
一堆数据点,有些难预测,有些容易预测
把容易预测的mse降低到一定程度后,再在容易点上优化,收益就变小了。那注意力就会转移到难预测的点上
如果用绝对值误差,收益永远不变,注意力就总在容易的点上了