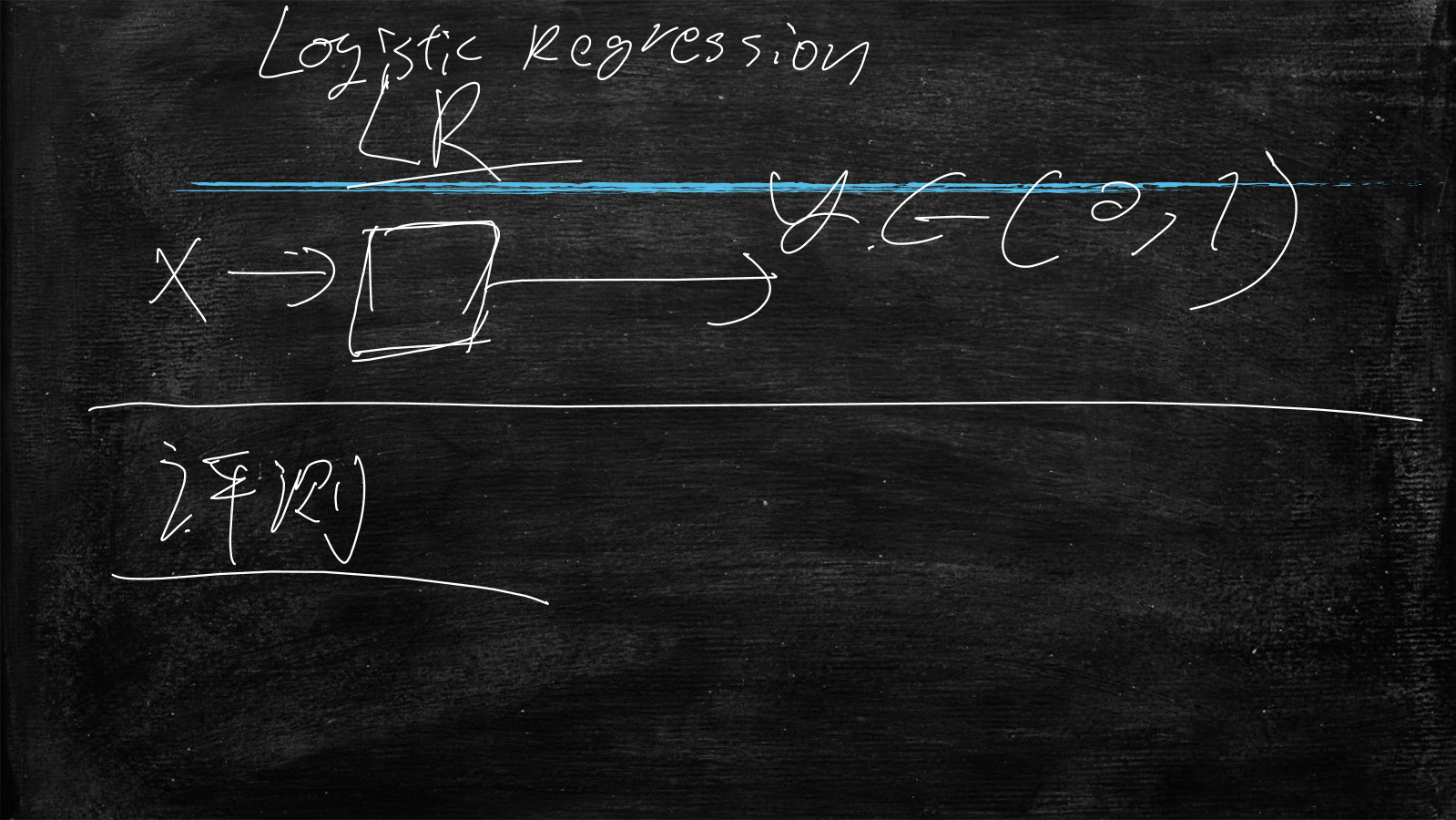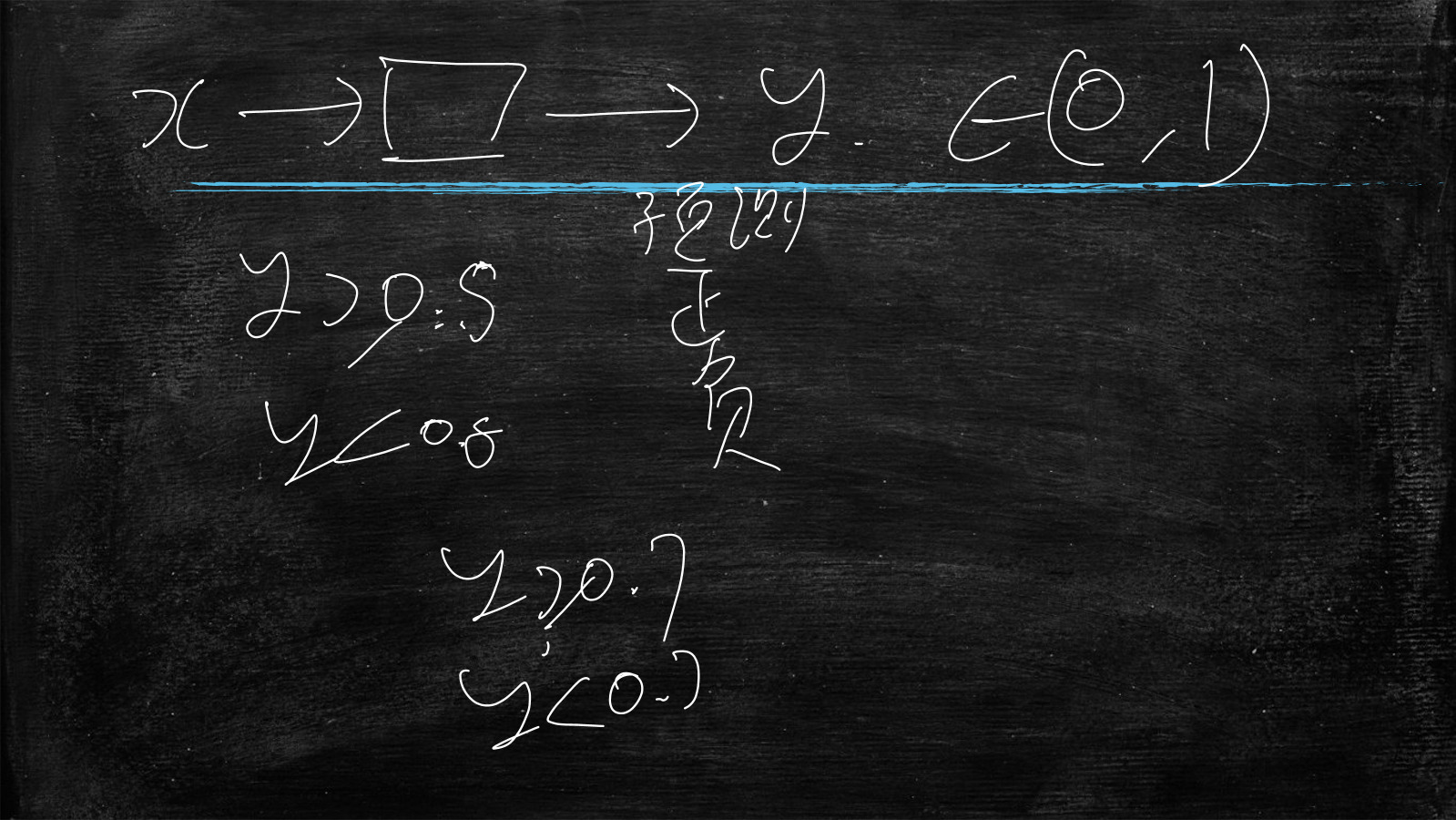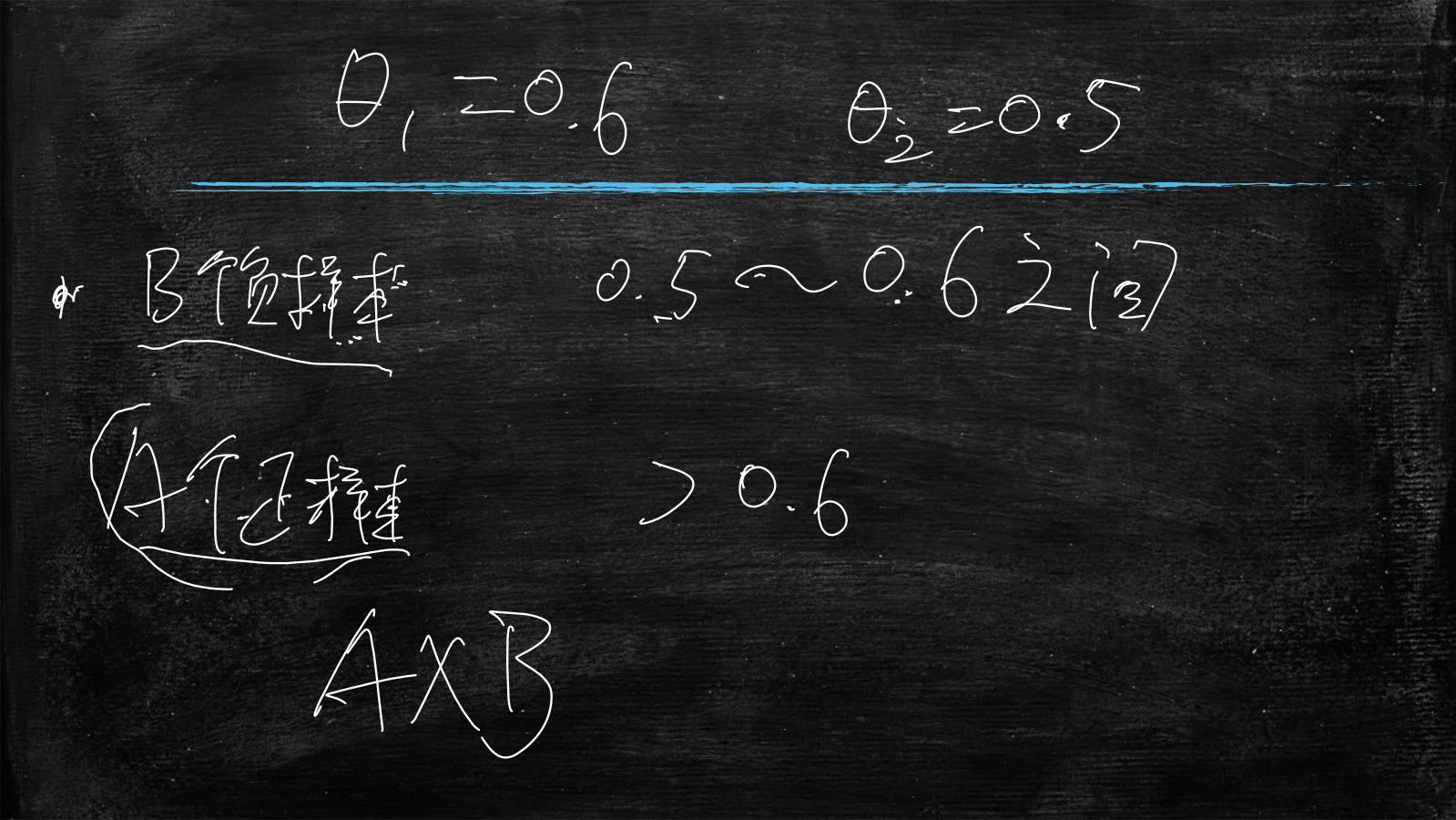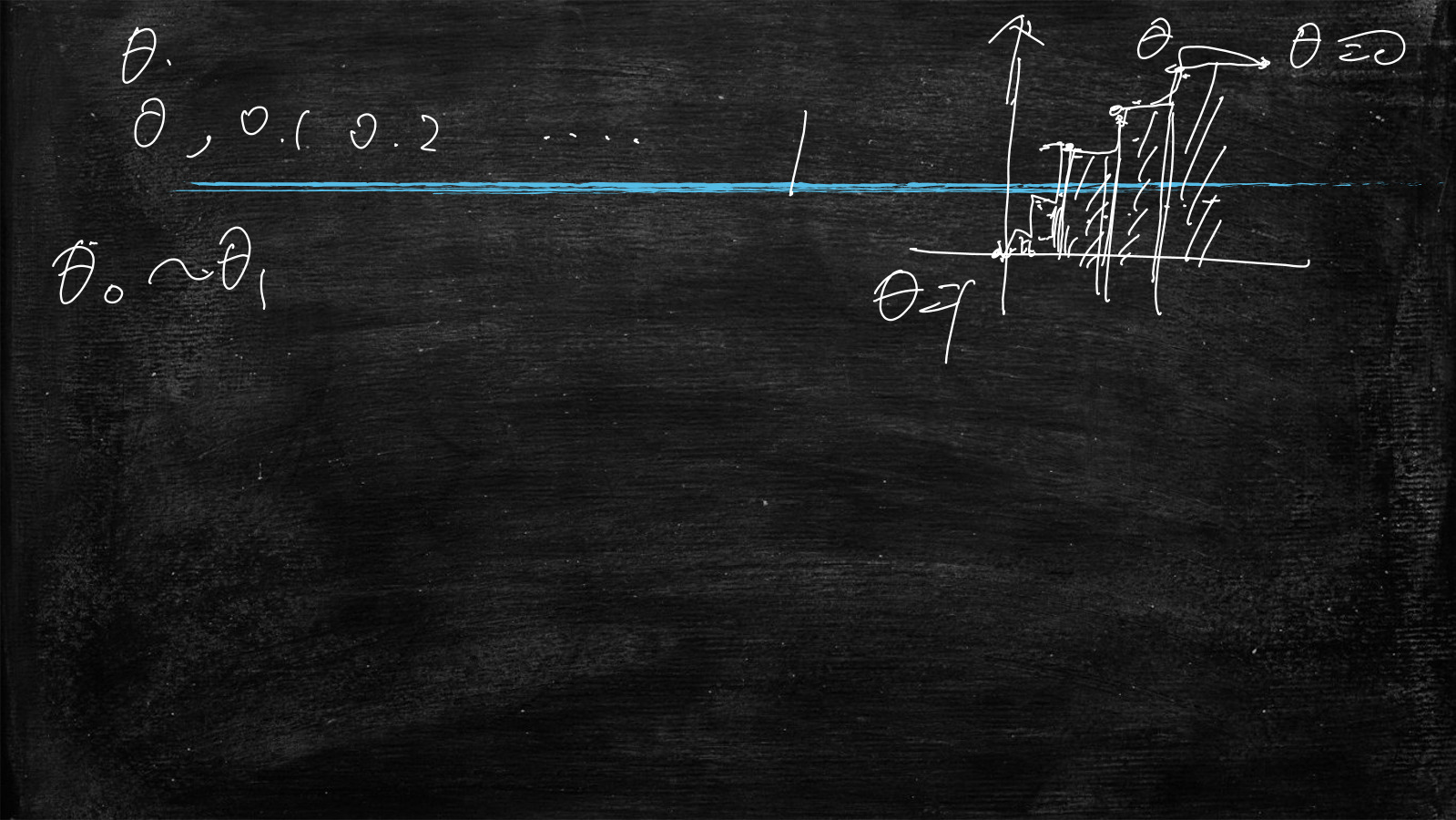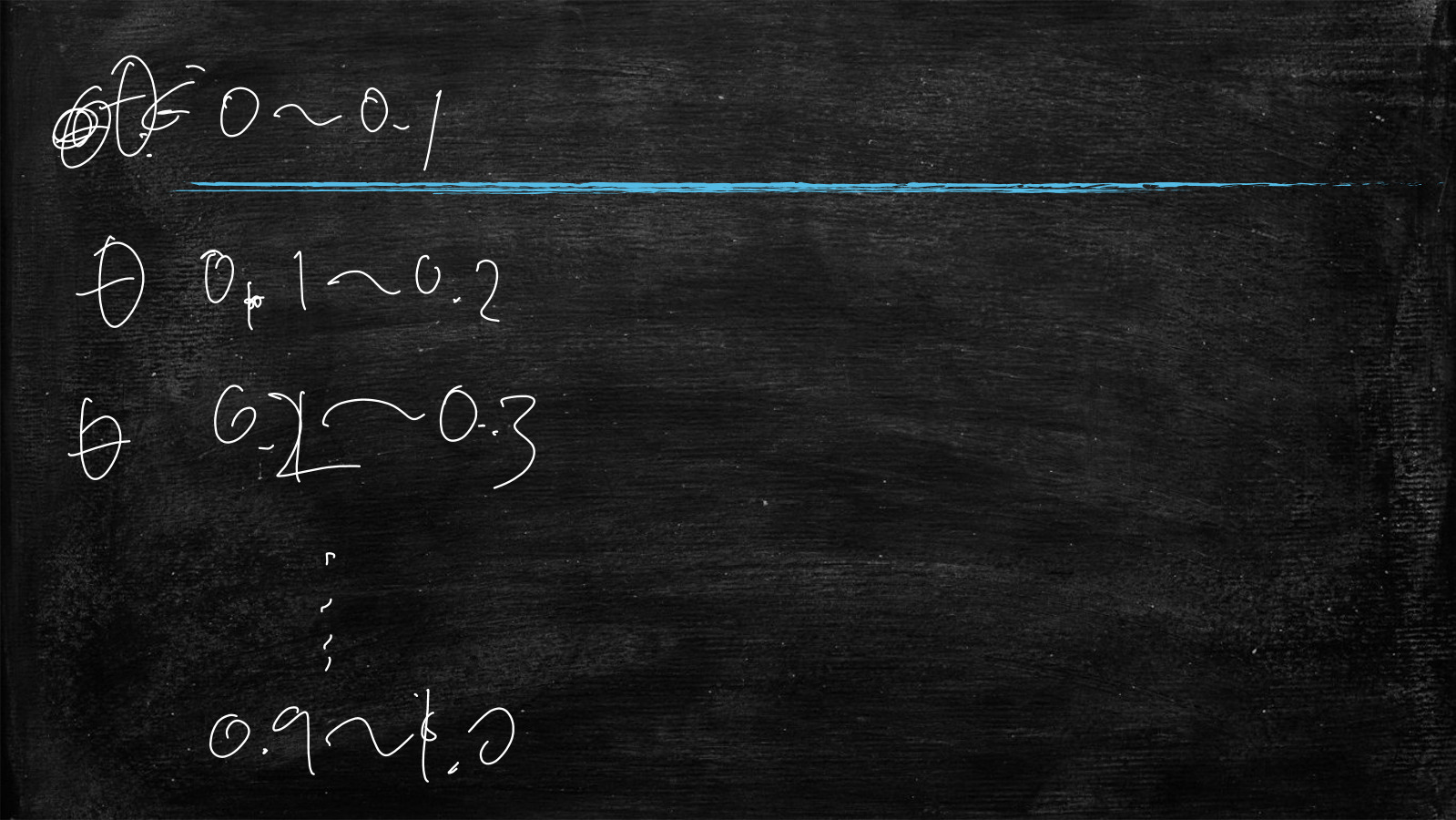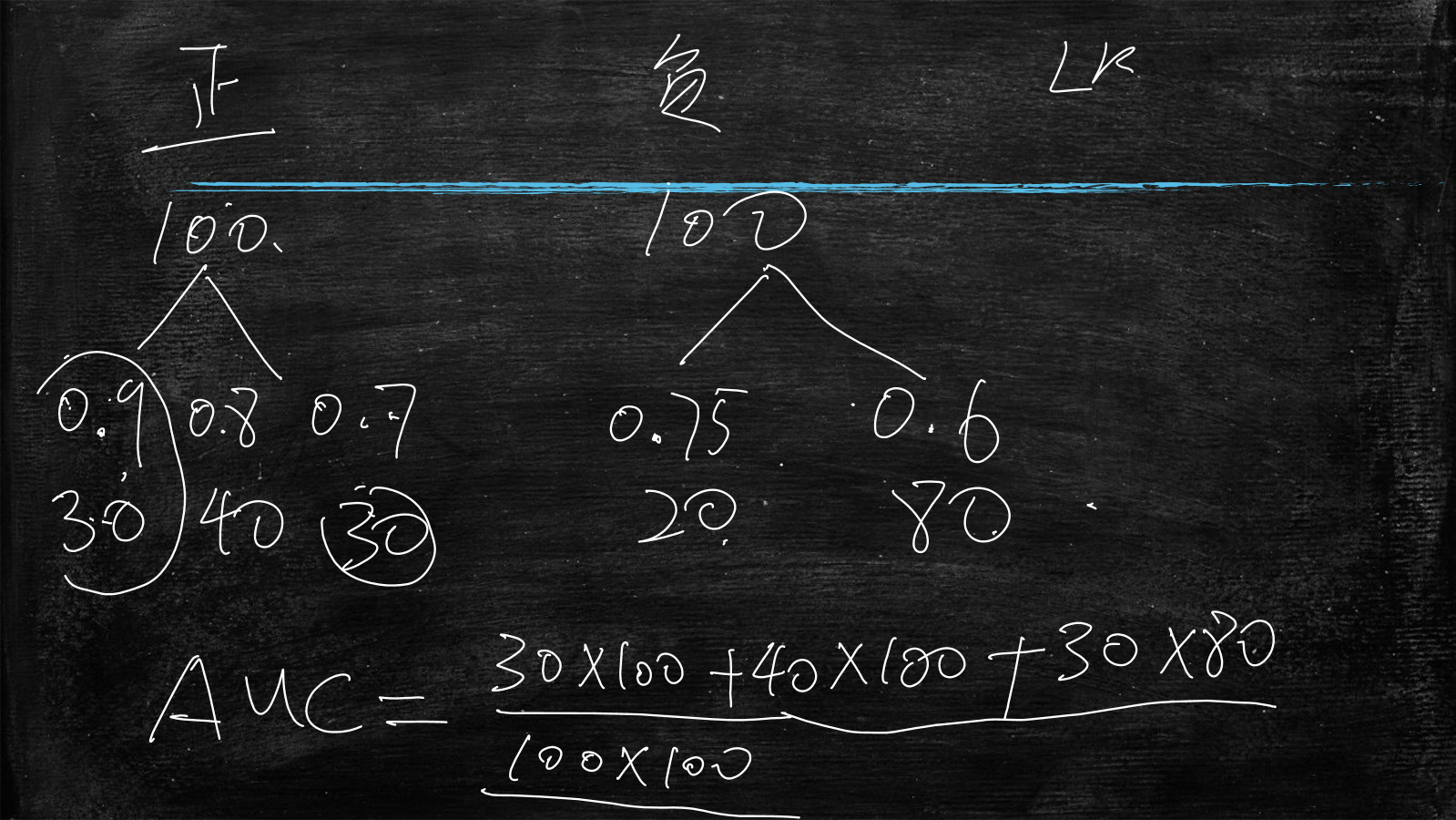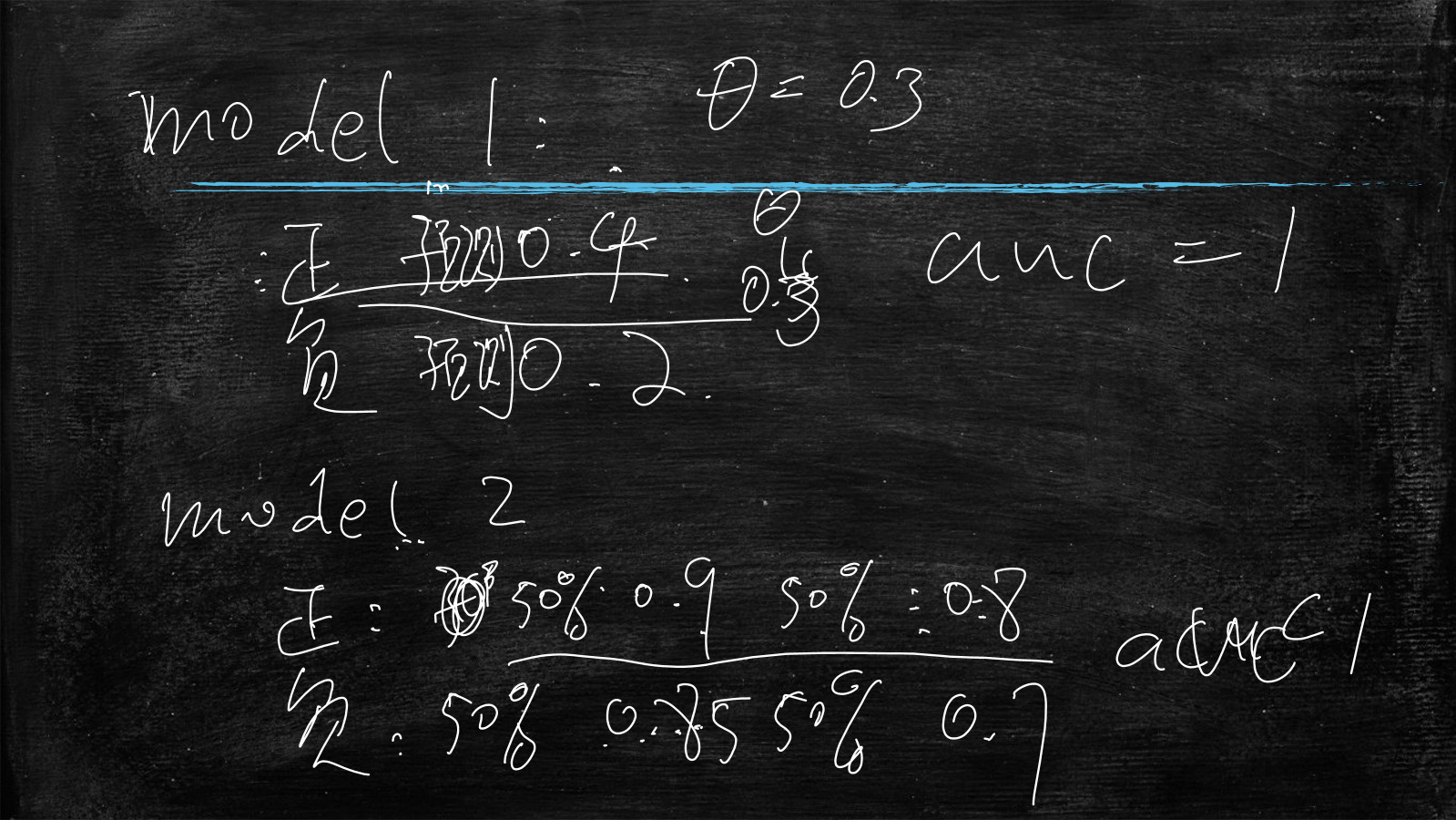# 到底好不好?模型评价指标讲解
之前5~6节已经讲完逻辑回归的主体框架
这节继续上节内容
逻辑回归做完以后,要有模型评价指标
比如:
向量x交由LR(逻辑回归模型-Logistic Regression)模型,输出y在(0,1)之间,不能等于0或者1,只能无限接近
任何分类模型都要有评测,要与正确答案进行比较的过程,就是评测
模型评测指标
分为三种
正确率
准确率和召回率
ROC曲线的AUC值衡量
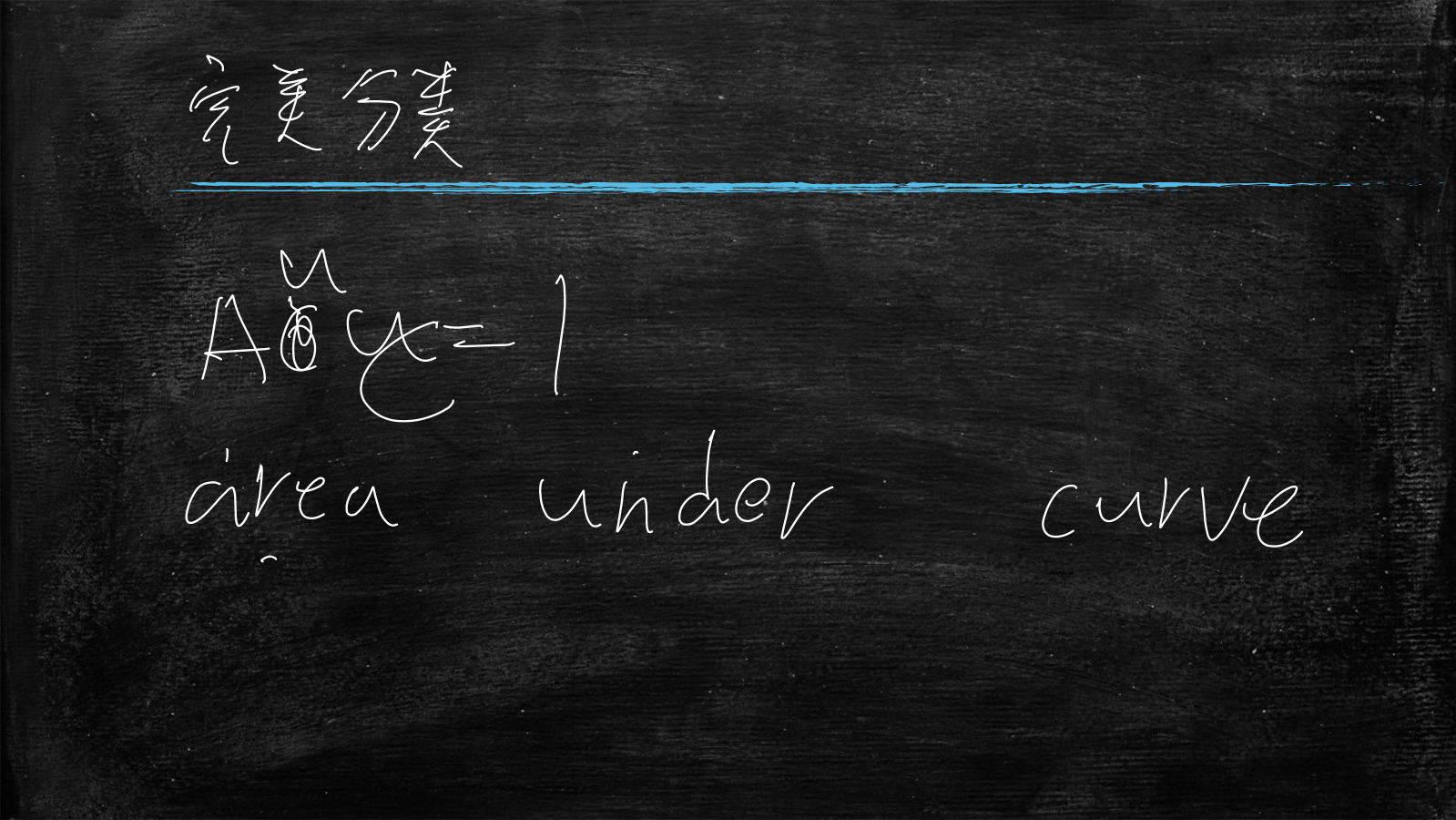
AUC是
Area Under Curve的缩写,即曲线下的面积
正确率
在逻辑回归模型中,正确答案有两种
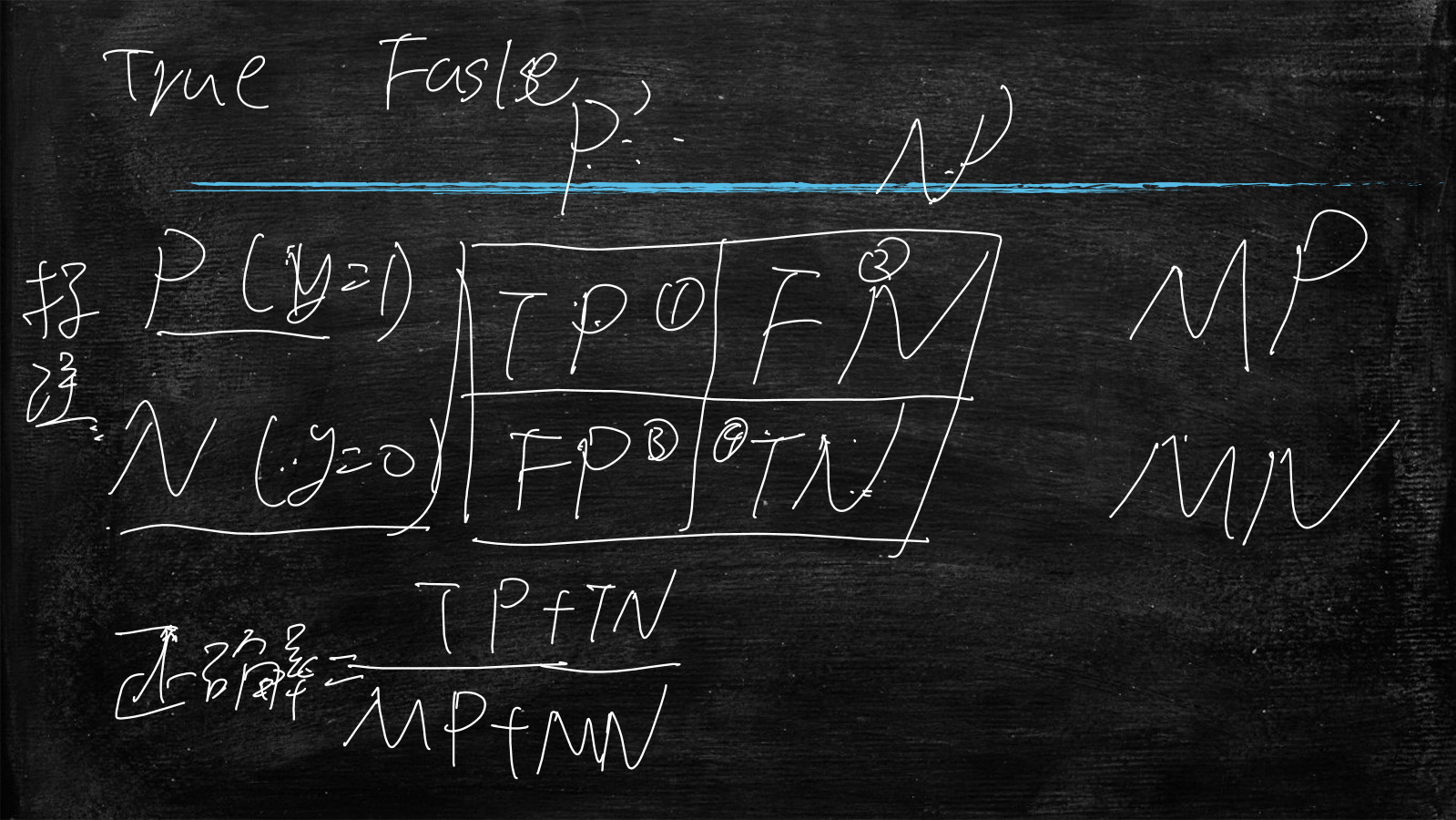
标注信息有两种情况,一种真实结果为1,一种真实结果为0
P(y=1)
N(y=0)
模型预测出来也有两种情况,一种预测结果为1,一种预测结果为0
P'(y=1)
N'(y=0)
这两两组合,就是四种情况
T是True 表示预测结果与真实结果一致,即为真
F是Flase 表示预测结果与真实结果不一致,即为假
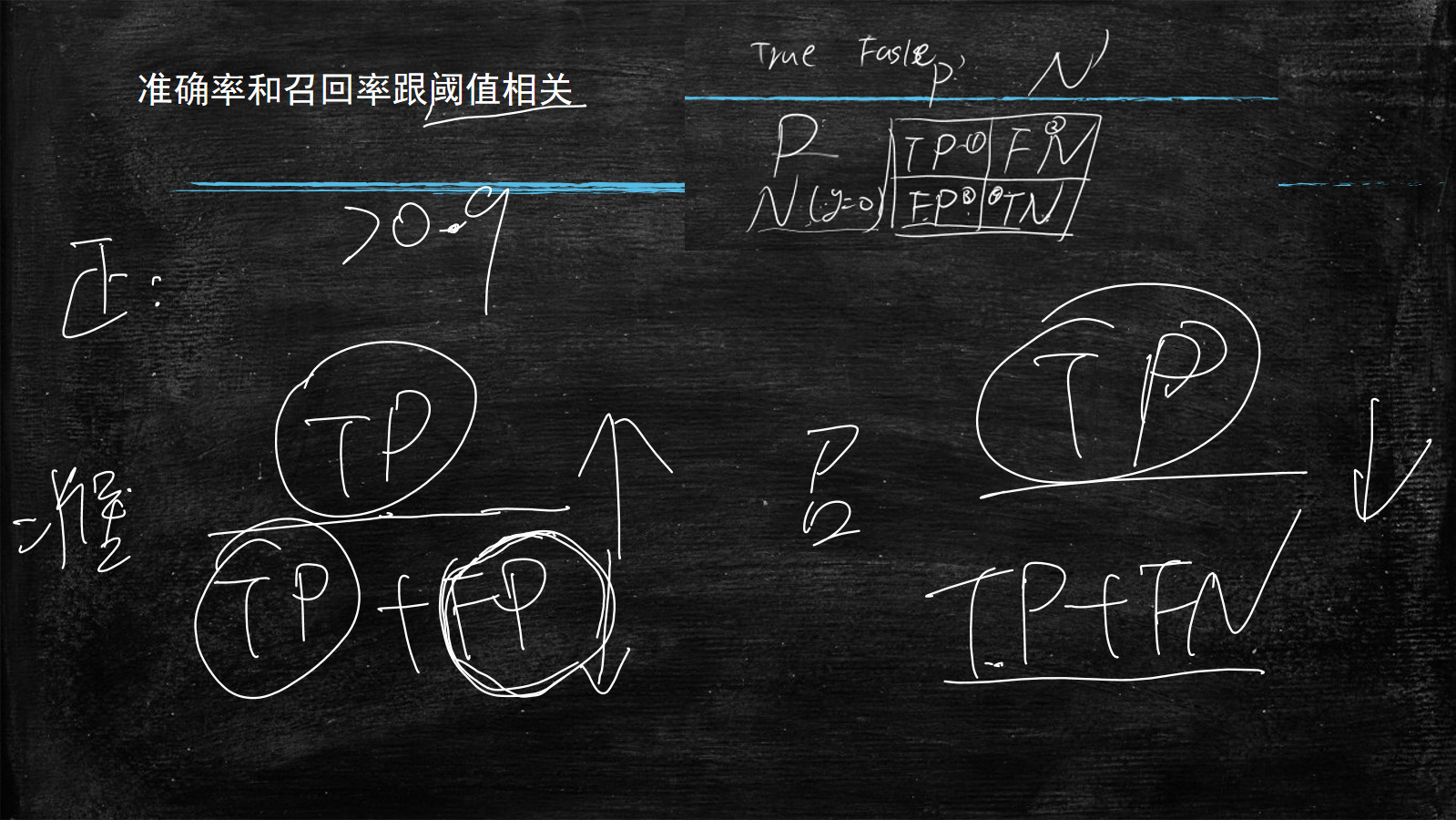
| P'(预测结果为1) | N'(预测结果为0) | ||
|---|---|---|---|
| P(真实结果为1) | TP(True_P)@1 真的预测为1 | FN(Flase_N)@2 假的预测为0 | |
| N(真实结果为0) | FP(Flase_P)@3 假的预测为1 | TN(True)N@4 真的预测为0 |
每个测试样本,必然在这4个(TP、FN、FP、TN)区间之内
模型越好,那么数据落在1、4区间越多,就是预测结果与真实结果一致的越多
比如,总共有M个正样本与m个负样本,总样本数量为MP+mN
那么正确率为:预测对的除以总样本数量
$$
正确率=\frac{TP+TN}{MP+mN}
$$
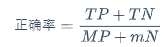
那么以正确率来评价模型有什么问题吗?
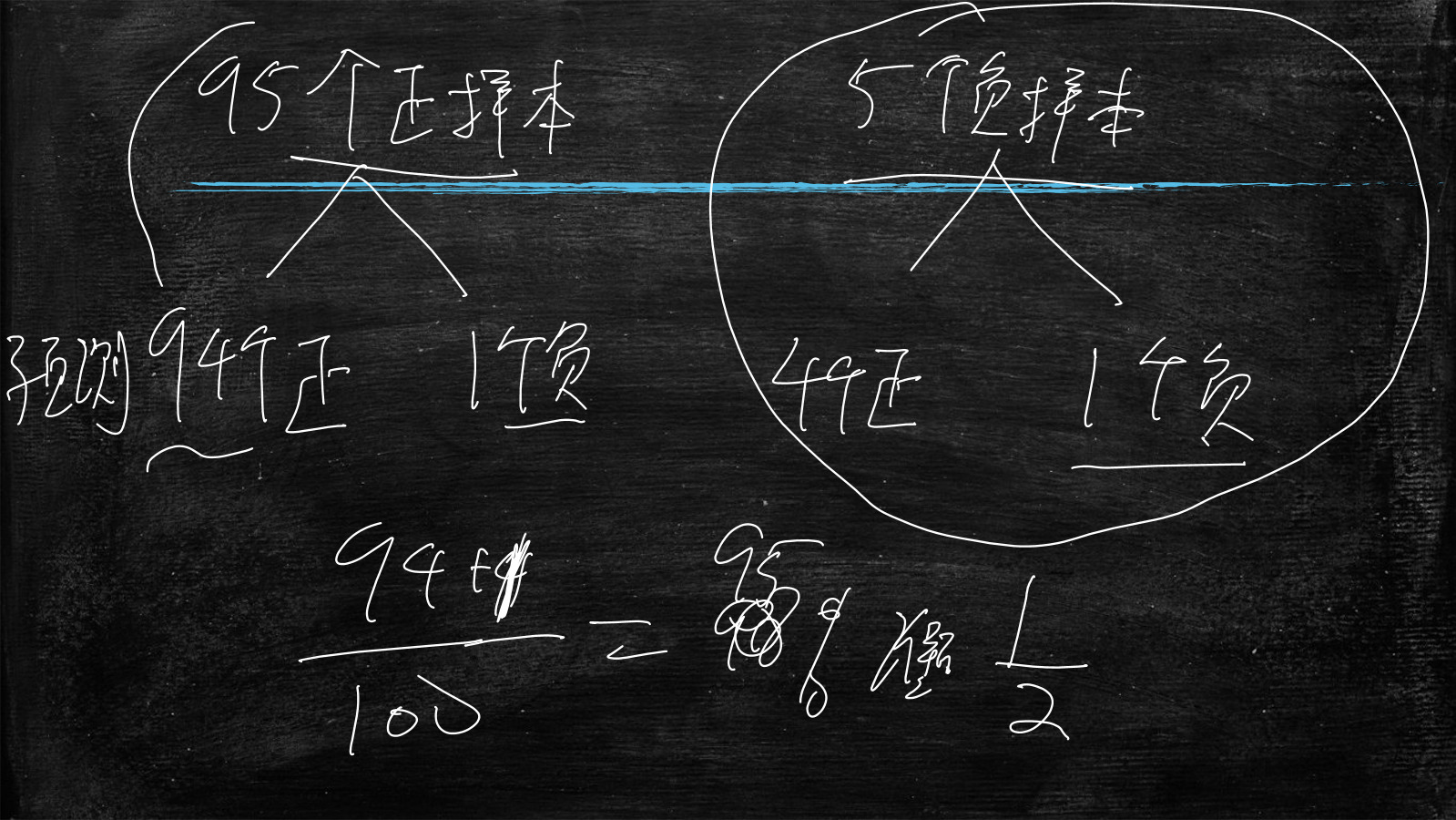
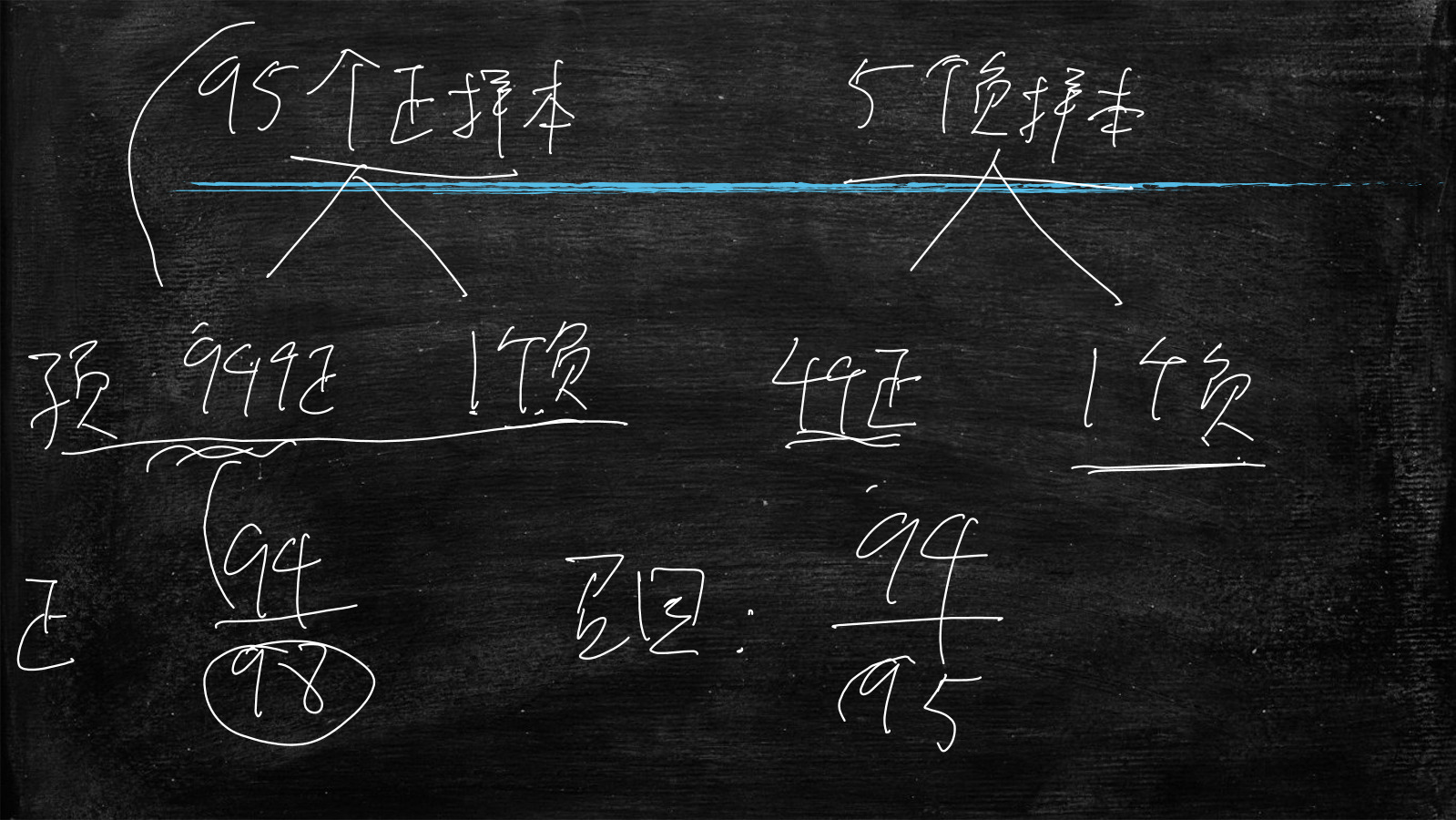
比如说,有95个正样本和5个负样本
正样本预测结果为94个正,1个负
负样本预测结果为4个正,1个负
那么正确率就是(94+1)/(95+5)=0.95
可以看出当它作为正样本分析时,正确率(94/95)还可以
但是作为负样本是,正确率(1/5)就有很大差异
答:存在当正、负样本数量不均衡时,正确率的差异会很大,这个评价标准是要看两边的
那么有没有只看一边的评价指标呢?
当预测是错误的:就只看错误的一边了,与TP和FP无关了
$$
\frac{TN}{FN+TN}
$$

准确率和召回率
准确率:预测为真的所有样本数量(TP+FP),其中预测为真和真实结果一致的数量所在比例为准确率
预测为正的样本中,和真实结果一致的数量比
$$
\frac{TP}{TP+FP}
$$
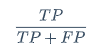
召回率:真实结果为真的所有样本数量(TP+FN),其中预测为真和真实结果一致的数量所在比例为召回率
实际中有多少个正样本,召回了几个
$$
\frac{TP}{TP+FN}
$$
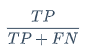
还是上面的例子:
有95个正样本和5个负样本
正样本预测结果为94个正,1个负
负样本预测结果为4个正,1个负
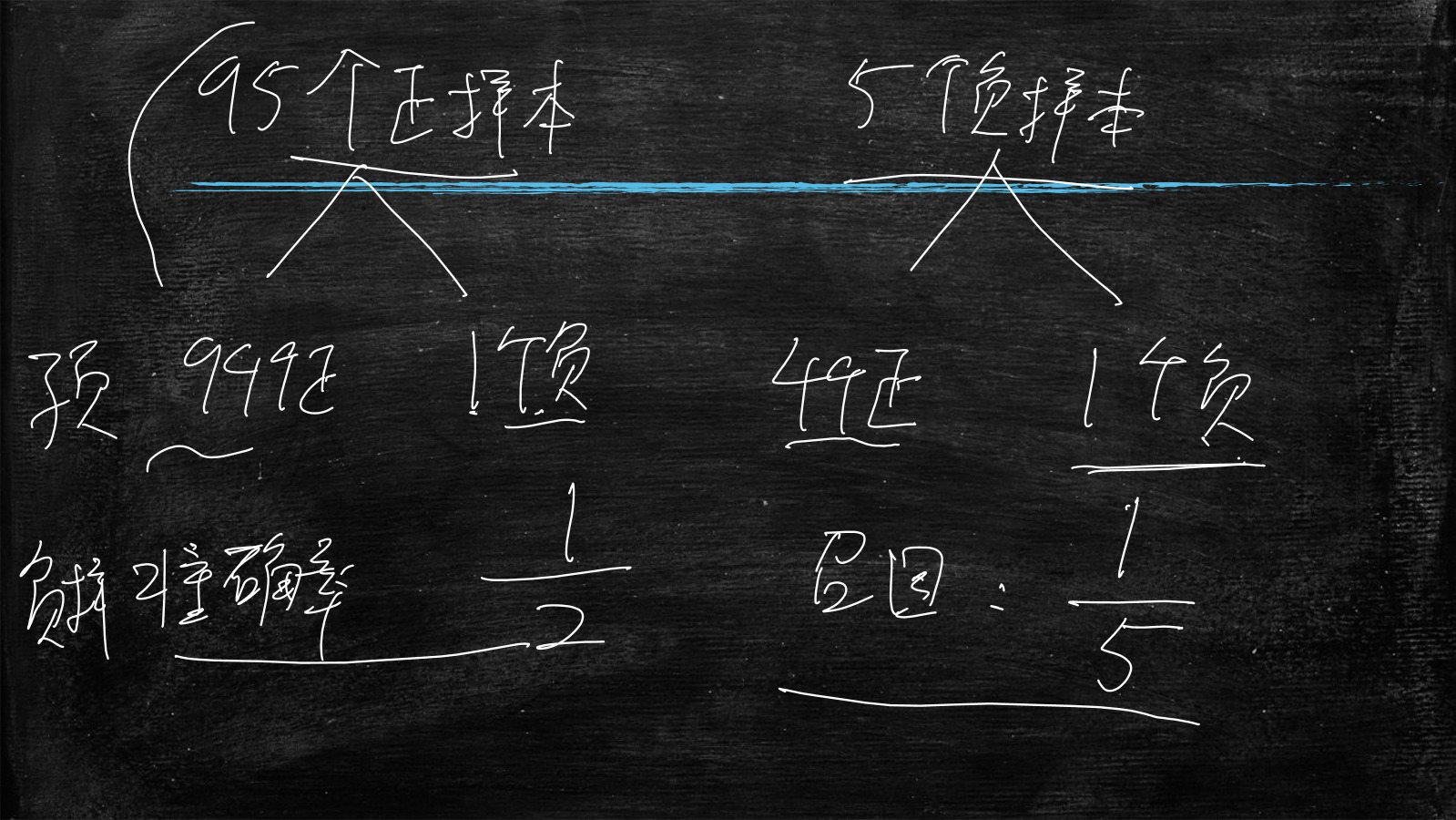
负样本
准确率为(负样本中预测为负的数量为1)/(正样本中预测为负1+负样本中预测为负1)=1/2
召回率为(负样本中预测为负的数量为1)/(负样本5)=1/5
刚才看了负样本,接下来再看正样本
正样本
准确率为(正样本中预测为正的数量为94)/(正样本中预测为正94+负样本中预测为正4)=94/98
召回率为(正样本中预测为正的数量为94)/(正样本95)=94/95
接下来,把模型出来的结果,从高到低的分值,按照从左到右排列,如下图所示
圆圈里为1的是正样本(真实结果)
圆圈里为0的是负样本(真实结果)
画竖线代表阈值,一般是0.5,若在线的左边为正,右边为负
那么随着画竖线越来越左,就会影响正样本的分布,从而证明这个准确率和召回率是和阈值有关的
因为准确率和召回率是看一边的,由于阈值的倾斜的导致,一边数据量可能增大可能减少,就会影响准确率和召回率
不同的阈值导致不同的预测结果,不同的预测结果对应着不同的准确率和召回率
因此,准确率和召回率是跟阈值相关的
那么当阈值变大
预测为真的样本的失误会下降,即FP变小,则准确率会变大
由于阈值变大,预测为真的样本会变小,而真实样本数量(TP+FN)不变,则召回率会变小
结论:阈值越高,准确率越高(更准确),召回率越低(容易漏掉)
反之,阈值越低,准确率越低(容易出错),召回率越高(不容易漏掉)
阈值跟产品形态有关
比如:
内容产品中,鉴别反动黄色暴力等信息时,就要求阈值适当降低,宁可错,但是不能漏掉
推荐系统中做的定制化推送信息,就要求阈值适当调高,保证精准投放,可以漏掉
 既然
既然准确率和召回率是跟阈值有关,而阈值的选择又依赖于产品形态
那么有没有不依赖阈值的评价指标呢?
比如:
真实的结果:正样本有M个,负样本为N个
预测为正样本:正样本中有m个被预测为正,负样本中有n个被预测为正
坐标系X横轴代表n/N即FP/FP+TN,取值范围是(0~1)
坐标系Y横轴代表m/M即TP/TP+FN,取值范围是(0~1)
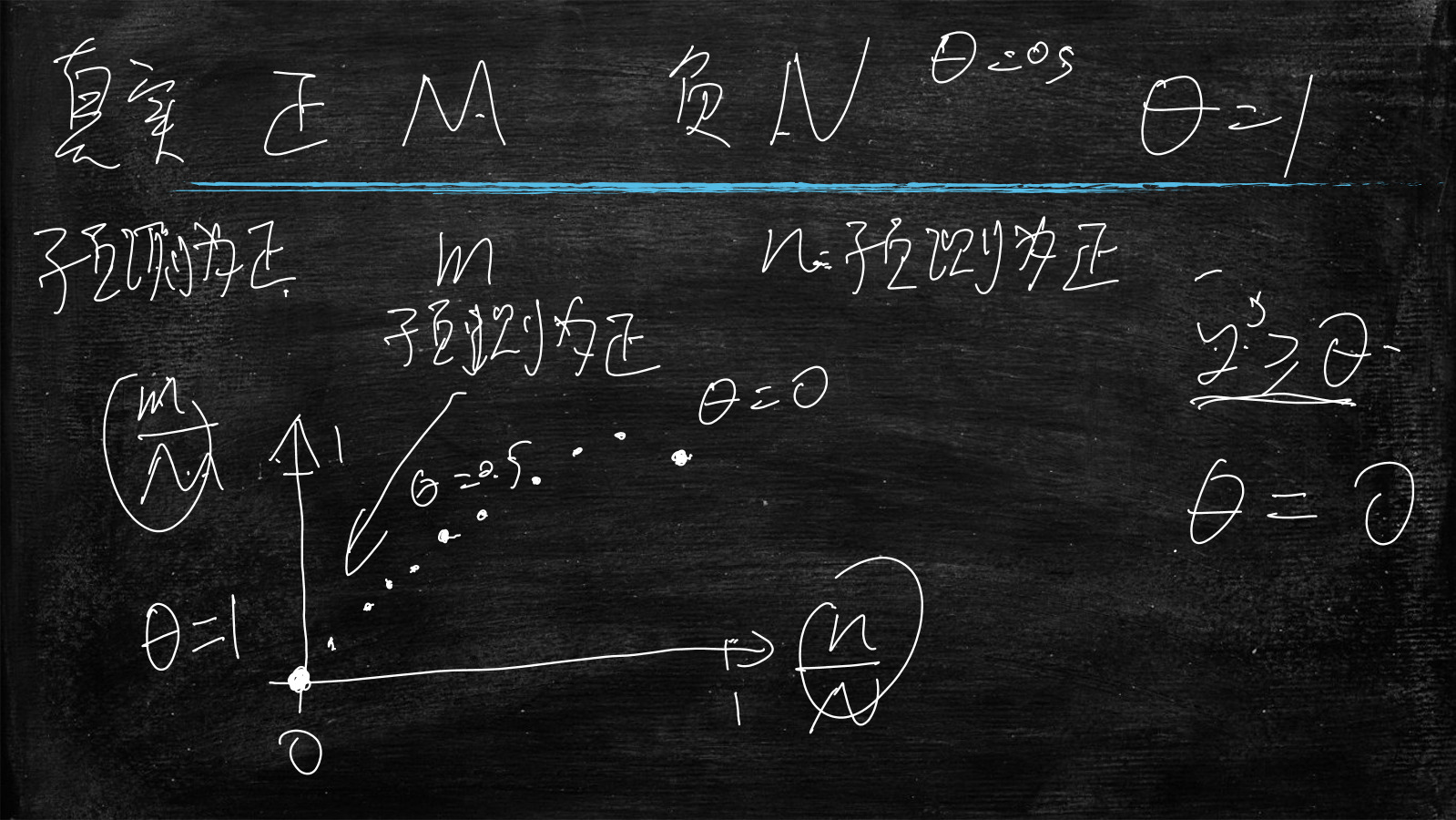
阈值为θ,预测分值为y',当y'>=θ,预测样本为正,反之预测为负
那么θ=0,则全部样本都预测为正,那么n/N=1以及m/M=1,所以当θ=0时,坐标系中为(1,1)
那么θ=1,则全部样本都预测为负,那么n/N=0以及m/M=0,所以当θ=1时,坐标系中为(0,0)
那么θ=0.5,坐标系中应该取中间的点
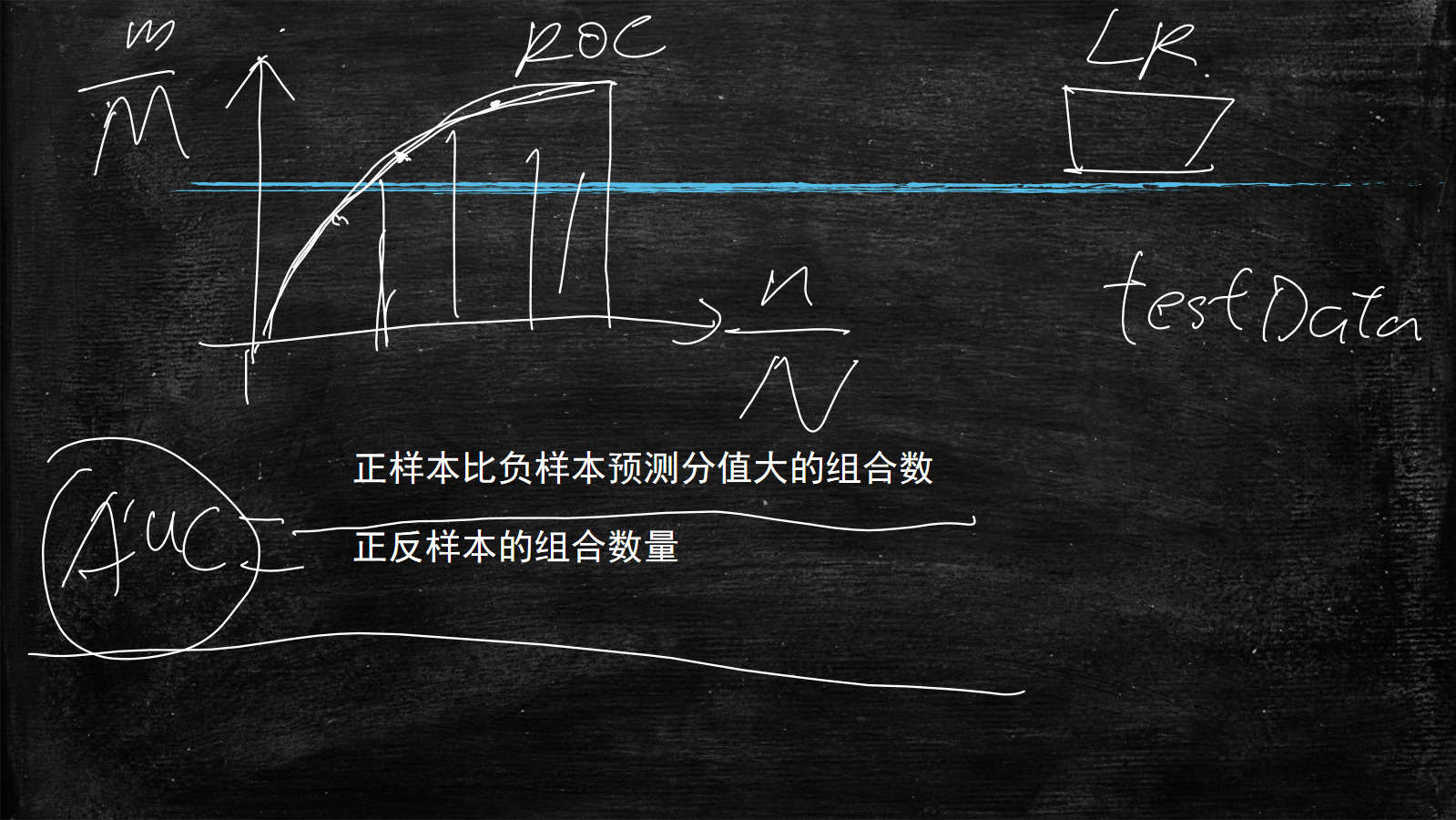
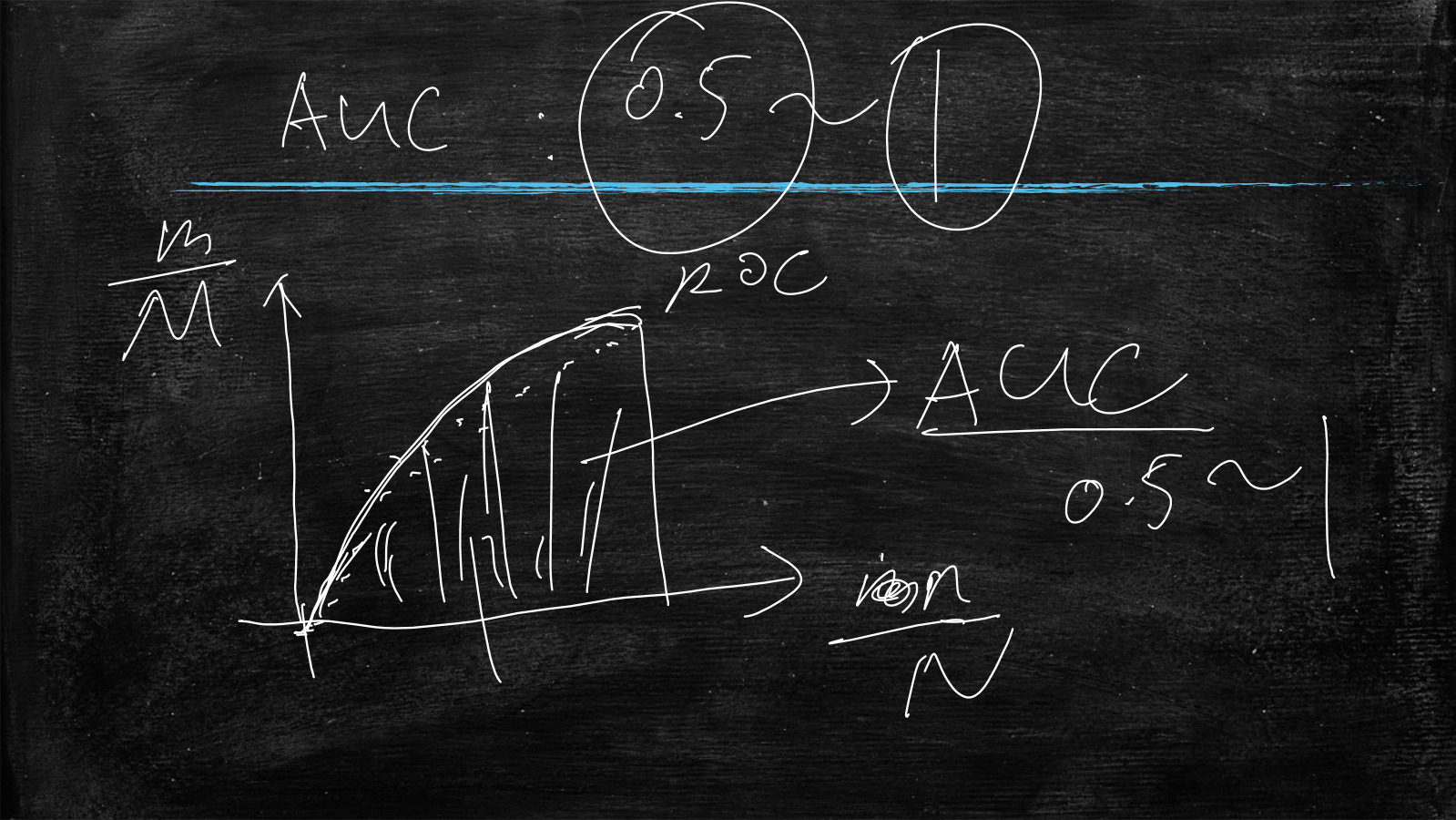
下图所示的虚线部分就是Roc曲线
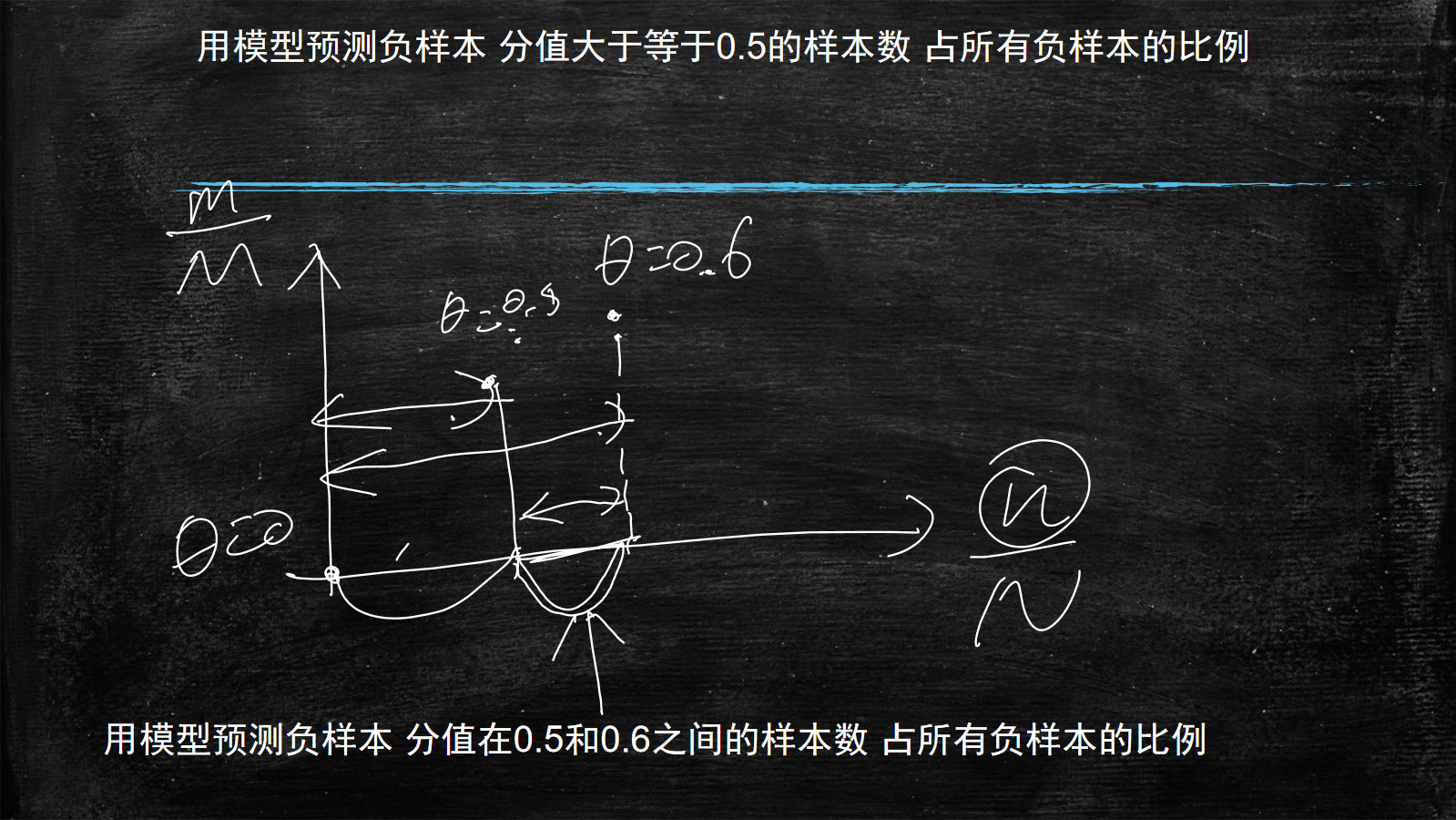
下图中所示的这段线段的长度代表:当θ=0.5时,n/N的值
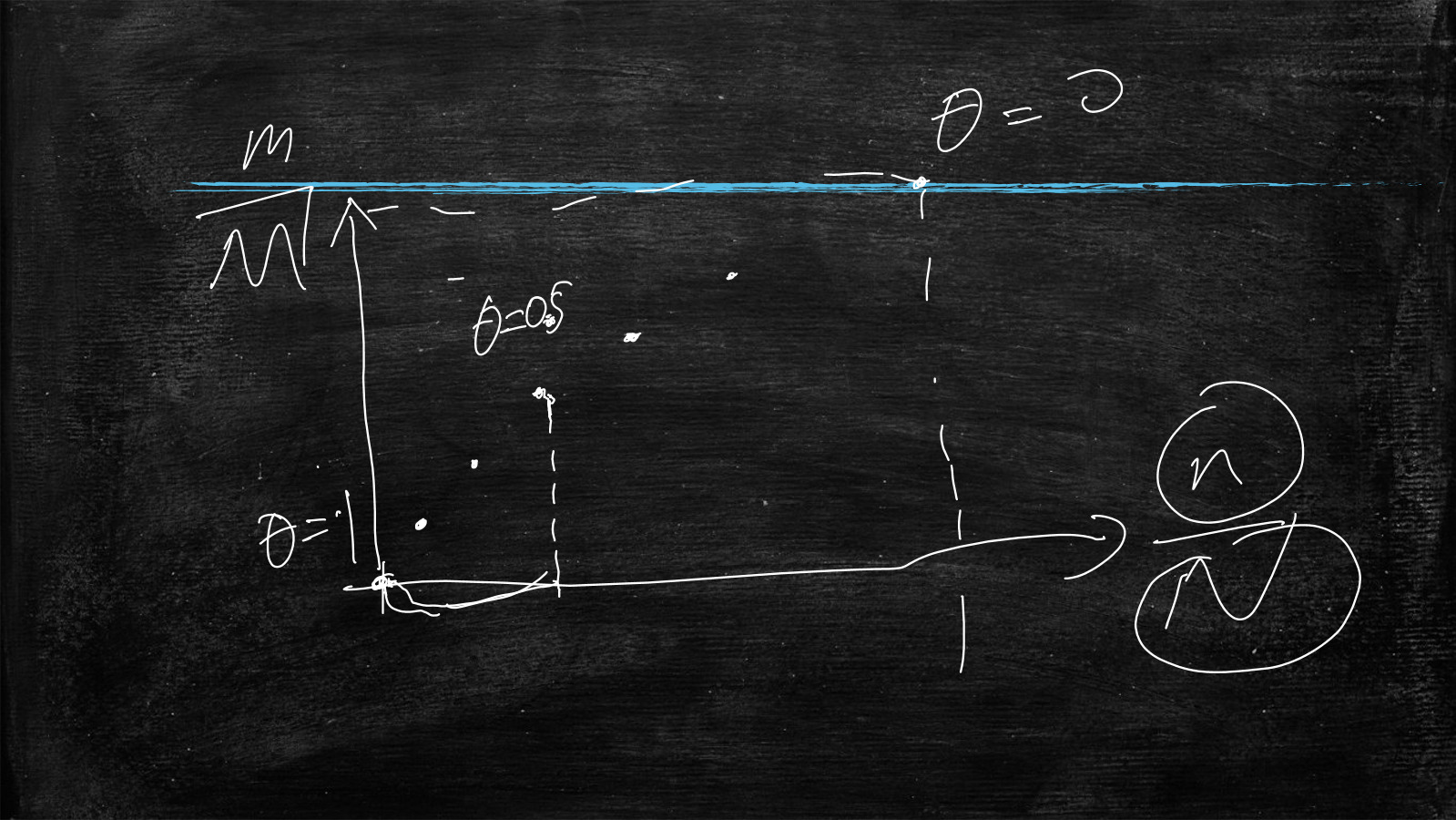 即:用模型预测负样本 分值大于等于
即:用模型预测负样本 分值大于等于0.5(θ)的样本数(n) 占所有负样本(N)的比例
下图所示为
用模型预测负样本 分值在0.5(θ)和0.6之间的样本数(n) 占所有负样本(N)的比例
模型预测正样本 分值大于θ1的数量 占正样本的比例
X轴的线段长度为
用模型预测负样本 分值在θ2和θ1之间的样本数(n) 占所有负样本(N)的比例
图中阴影部分为面积就是Y轴的线段高度乘以X轴的线段长度
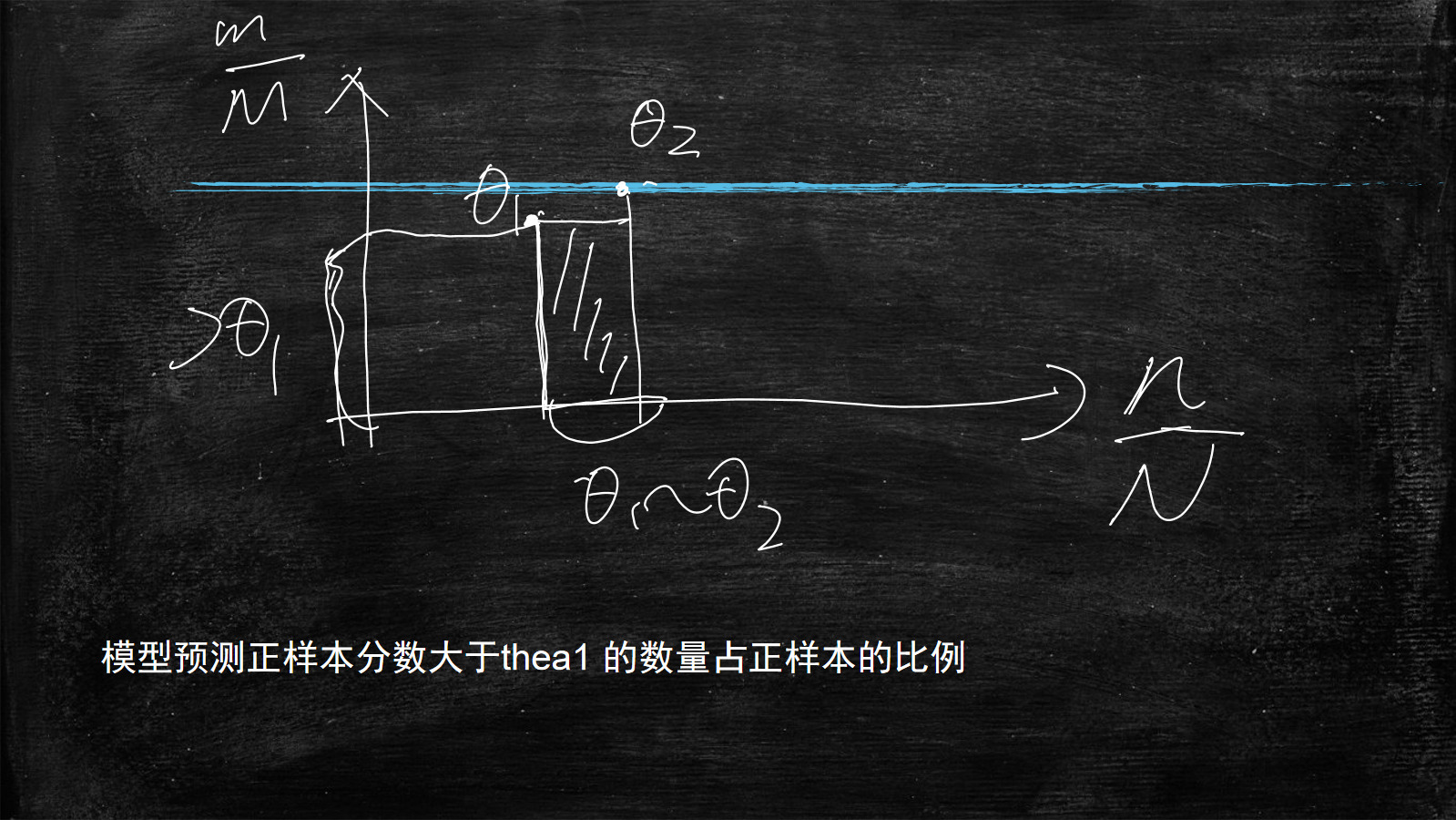 那么这个阴影面积的物理意义是什么呢?
$$
\frac{正样本中大于 \theta \times 负样本中在{\theta2-\theta1}之间}{M \times N}
$$
那么这个阴影面积的物理意义是什么呢?
$$
\frac{正样本中大于 \theta \times 负样本中在{\theta2-\theta1}之间}{M \times N}
$$
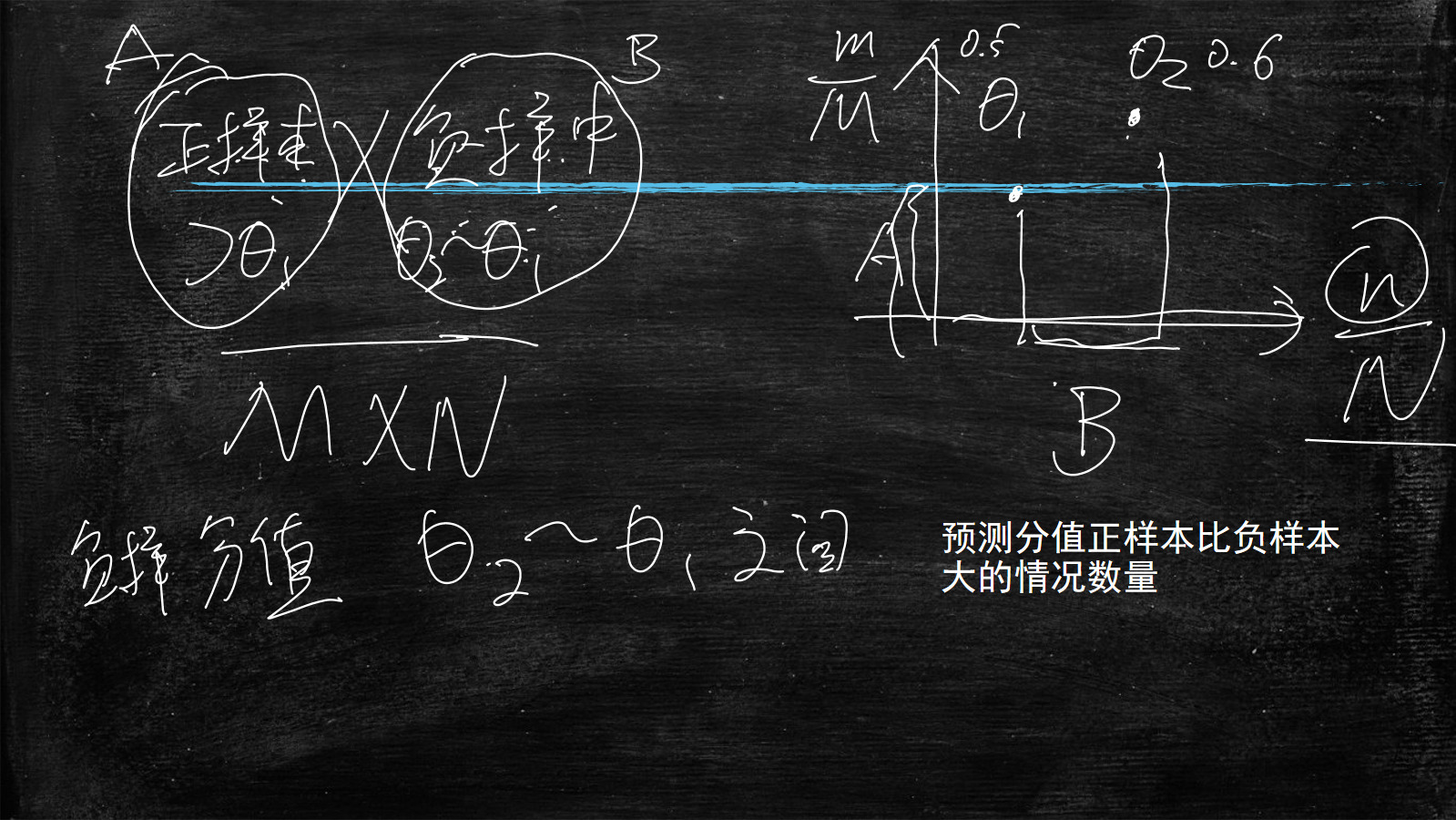
 $$
A=正样本中大于 \theta \qquad B=负样本中在{\theta2-\theta1}之间
$$
$$
A=正样本中大于 \theta \qquad B=负样本中在{\theta2-\theta1}之间
$$
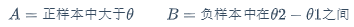
就能理解为:负样本中,预测分值在θ2和θ1之间的样本数,与正样本中,预测分值大于θ1(就是比前者大)的组合数
即:预测分值正样本比负样本大的情况组合数
有B个负样本的分值在0.5~0.6之间
A个正样本的分值大于0.6
那么预测分值正样本比负样本大的所有情况数量为:A乘以B
可以求出很多个小的阴影面积,当θ无穷的分下去(θ的取值区间特别的小),则图中的线段会变为曲线
θ的取值区间,每个这样的区间对应上图的阴影面积
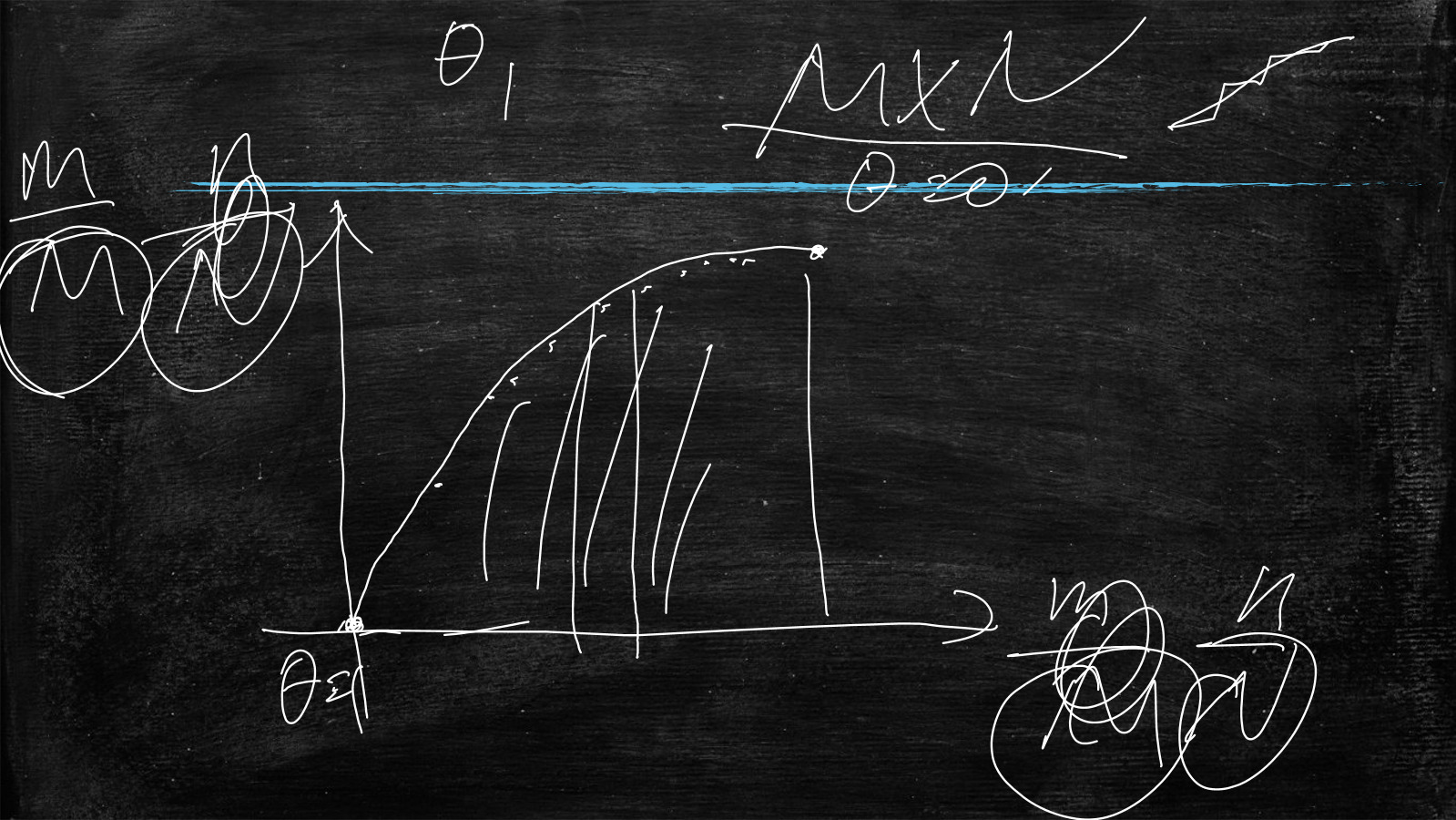 曲线下面的面积是什么意思呢?
$$
Auc=\frac{正样本比负样本预测分值大的组合数}{正反样本的组合数量}
$$
曲线下面的面积是什么意思呢?
$$
Auc=\frac{正样本比负样本预测分值大的组合数}{正反样本的组合数量}
$$

 有个训练好的逻辑分类器,遍历所有的
有个训练好的逻辑分类器,遍历所有的阈值,从0到1,得出很多的点,点可以连成一条曲线
那么曲线的面积表示就是
这条曲线就是Roc曲线
该曲线下的面积就是Auc
答:无关
如下图所示
正样本(100个),其中预测为0.9的样本数为30,预测为0.8的样本数为40,预测为0.7的样本数为30
负样本(100个),其中预测为0.75的样本数为20,预测为0.6的样本数为80
所以跟阈值没有关系
Auc是Area Under Curve,即曲线下面的面积
Auc值越高则分类模型越好
最低是0,代表负样本中预测的分数全部比正样本中预测的分数高,也就是全错了
其实对于二分类来说,就是把预测的结果完全反过来就行了,即:完全错取反就是完全对
所以,Auc的范围是(0.5~1)
1代表模型分类非常对
0.5代表模型没有任何意义,类似于随机蒙
Auc值是反映模型的真实能力的,与产品形态即阈值没有关系
model1
正样本中100%预测分值是0.4
负样本中100%预测分值是0.2
那么Auc=1,因为当阈值θ=0.3时,就能分类清晰
model2
正样本中50%预测分值是0.9,50%预测分值是0.8
负样本中50%预测分值是0.85,50%预测分值是0.7
那么Auc<1
由此可以看出,模型好坏在于区分度,也就是Auc表示的正样本预测分值整体要比负样本预测分值大
正确率:
问题:容易被两类不均衡所影响 指标被阈值所影响准确率和召回率:
特点:单独看一类预测结果的指标问题:指标被阈值所影响Roc曲线和Auc值:
特点:真正反映了模型的能力,表达了正负样本数的区分度,理论值为(0.5~1),实际值一般是(0.7~0.85)问题:推理过程不好理解