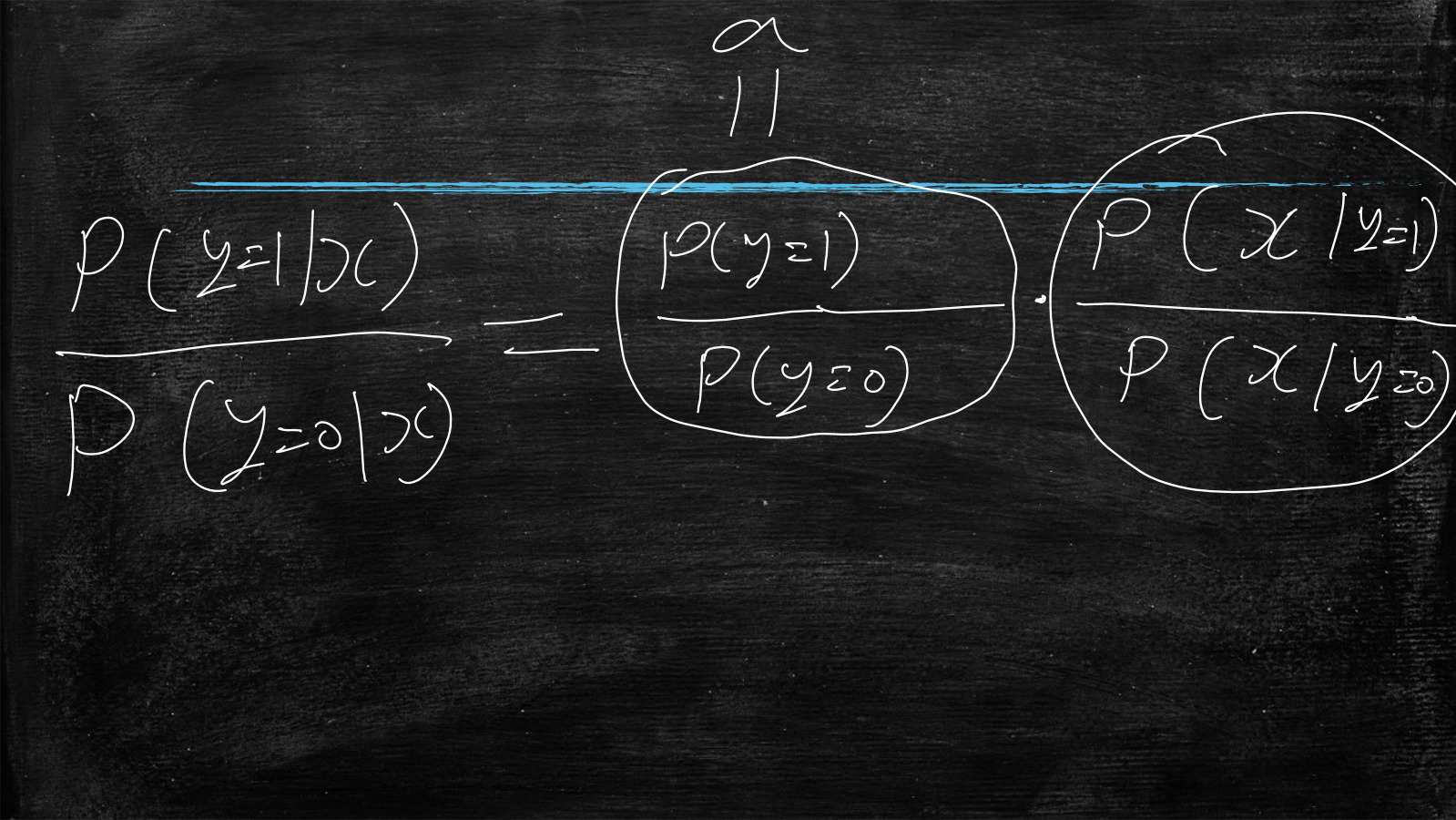ShiYu

# 让学习更高效，数值优化和一只看不见的手

解决遗留的问题 这个逻辑函数是将wx压缩在(0~1)0到1之间，那么这个逻辑函数是唯一的吗？

当然不是唯一的，那么为什么要选这个逻辑函数呢？

是因为效果好，通过工程上大量试验得出的，符合客观规律 image-86

接下来就讲解为什么要选上面的逻辑函数了？

先铺垫些数学

下图所示，均匀分布，0~2之间的值的概率是一样的，面积是总概率和为1，Y轴的高度为概率密度，X轴是连续的取值

image-86

概率是概率密度乘以x值(长度)

概率为0的事件一定不能发生吗？

答：会发生，在数学上，当x取值为具体的点时，比如x=1.5时，长度为0，那么0x1/2=0，概率为0

image-86

定义必须清楚

image-86

刚才说的时均匀分布，接下来是高斯分布(正态分布)

就像一口钟一样

当x等于image-20220316160922763时，概率密度最大

image-86

image-20220316160947924决定钟口的大小(x的分散程度)，值越大钟口越大(x的分散程度大)，值越小钟口越小(x的分散程度小)

根据概率论：曲线底下的面积等于1

image-86

一元高斯

均值image-20220316160922763、均方差image-20220316160947924

在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式： image-20220317145428526

img为总体方差，img为变量，img为总体均值，img为总体例数。 image-20220317145448598

正态分布是机器学习的先验条件

image-86

在机器学习里有这个假设：是不需要证明的，即：公理

对于具体一个类别来说，它的特征分布符合正态分布

image-86

比如：中国男性身高的分布

均值image-20220316160922763=1.71

均方差image-20220316160947924=20

x=1.8

f(x)=0.2

身高为1.8的中国男性，占全国中国男性的比例为0.2

image-86

对于中国男性来说，有自己的均值和方差

对于中国女性来说，也有自己的均值和方差

对于上海男性来说，也有自己的均值和方差

image-86

拿身高举例

分为男性(f(x|y=男1))与女性(f(x|y=女0))的分布情况

由于统计学上证明，男的方差与女的方差是一样的以下公式不做区分了

男性分布公式： image-20220317152228733

女性分布公式： image-20220317152245755

image-20220317152021201代表男性身高均值

image-20220317152046960代表女性身高均值

image-86

那么现在有个身高样本值x=170cm，判断是男还是女？这种就是分类问题

当x成立时，它是男性的概率为P(y=1|x)，它是女性的概率为P(y=0|x)

根据贝叶斯公式： image-20220317154626809

那么P(x)是170cm占总人口的比例这个不好知道，所以想着要约掉它，就想到了将P(y=1|x)与P(y=0|x)相除

image-86

P(y=1|x)与P(y=0|x)相除 image-20220317153950336

P(x|y=1)是男性身高的概率分布函数

P(x|y=0)是女性身高的概率分布函数

image-86

代入公式： image-20220317171545625

image-86

image-86

P(y=1|x)+P(y=0|x)=1相加概率为1，代入公式： image-20220317171610166

image-86

image-86

image-86

接着代数运算： image-20220317175042327

运算到此处是不是很眼熟了？

这就是逻辑回归函数，其实就是在学习w与w0

image-20220317173409628

image-86

因此：逻辑回归要承认两个事实

  • 满足正态分布
  • 两类数量相等，a=1 P(y=1)=P(y=0)这也是为啥需要上、下采样来满足数量相等的根本原因

image-86

那么P(x|y=1)与P(x|y=0)这两个能求出吗？也就是求出image-20220317152021201image-20220317152046960image-20220316160947924

答：不能求出，因为未知数是三个项，但是只有两个方程，未知数多于方程式，

image-20220317173409628

所以，求解不出

虽然P(x|y=1)是男性在170cm的比例与P(x|y=0)是女性在170cm的比例求解不出，但是它们两者的差异是能知道的，全部的不知道，只知道部分的

image-86

所以这个也是判别模型，就是说虽然不知道上面两个的分布情况，但是用来做判别是够的，因为做分类用的信息相对来说是少的

当别人问逻辑函数中的e怎么来的？就是从正态分布中来的，因为逻辑回归假设的正态分布

image-86

那么，到底是先知道的原因(上面的推理过程)，才有了这个逻辑回归；还是先知道了逻辑回归，才有了原因呢？

这个不好说，作为思考题

就像，一开始人们扔铅球，通过大量的试验，得出了最佳的投射角度，他们根本不知道力学的原因，但也能找出结果

实际工程做的非常好的人，未必能搞定原理

但是搞不定力学，人们还是能扔好铅球，但是永远不能把卫星送上天

所以还是要懂原理的

image-86

还有一个遗留问题

损失函数为什么选择KL距离？ image-20220317180704581

image-86

接下来分析KL距离怎么来的？

引出最大似然估计：

任何一件事情y对应的概率为w，虽然w并不知道，但是我们能得到很多的结果x

也就是说，虽然不知道原因，但是能知道原因产生的结果，原因是通过概率来产生的

那么怎么才能找到这个概率w呢？能让这些结果x发生概率最大的w，就是一个好的w

image-86

做机器学习时，拿到了很多对x,y，这些数据是已经发生的，所以需要这个所有概率的发生最大化，是个累乘的过程： image-20220317182359554

image-86

代数运算： image-20220317182803535

两边取log将累乘变为累加log(a b c d)=loga+logb+logc+logd image-20220317183229224

image-86

logP(xi)是个自然分布，我们更多的是找x与y的关系，所以主要看这个，让它最大 image-20220317183739698

image-86

P(y=1|x)与P(y=0|x)代入公式 image-20220317184432209

image-86

P(y|x)代入 image-20220317184916812

image-86

image-20220317185155756

image-20220317180704581

这个公式是不是就是KL距离呢

image-86

总结：

  • 逻辑回归的逻辑函数是通过正态分布得出，前提是正负样本相等
  • 损失函数KL距离函数是通过最大似然估计得出的

← 朴素贝叶斯模型：简单背后蕴含的有效 →