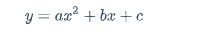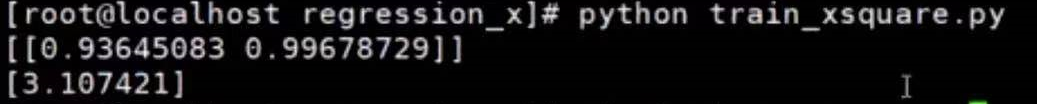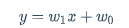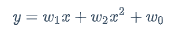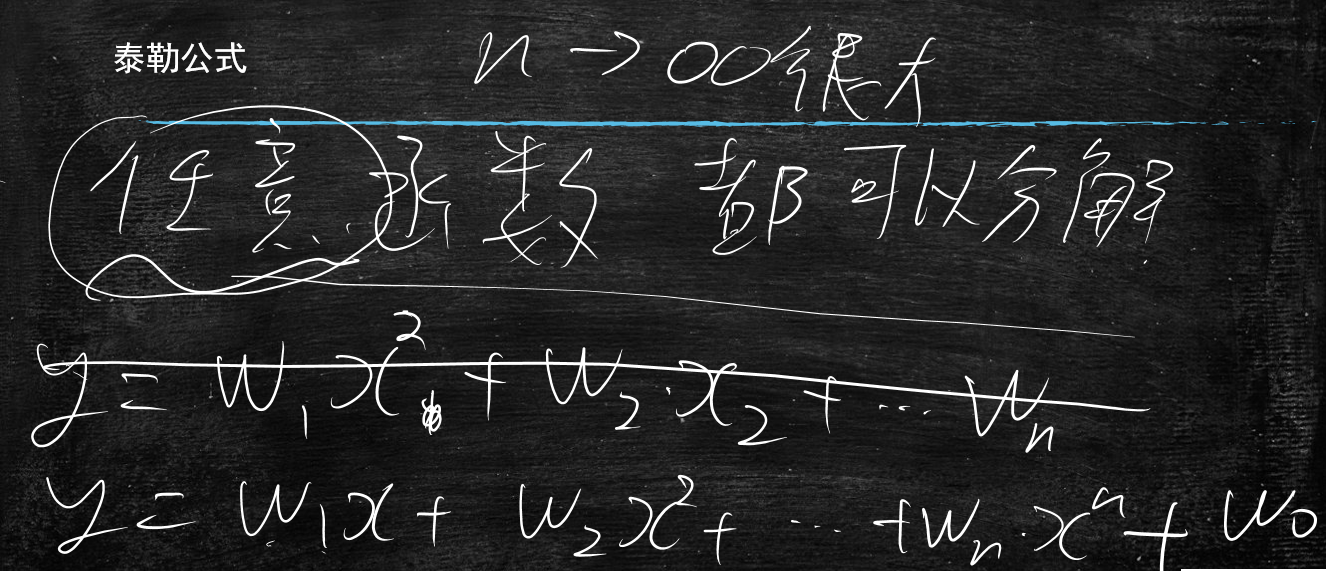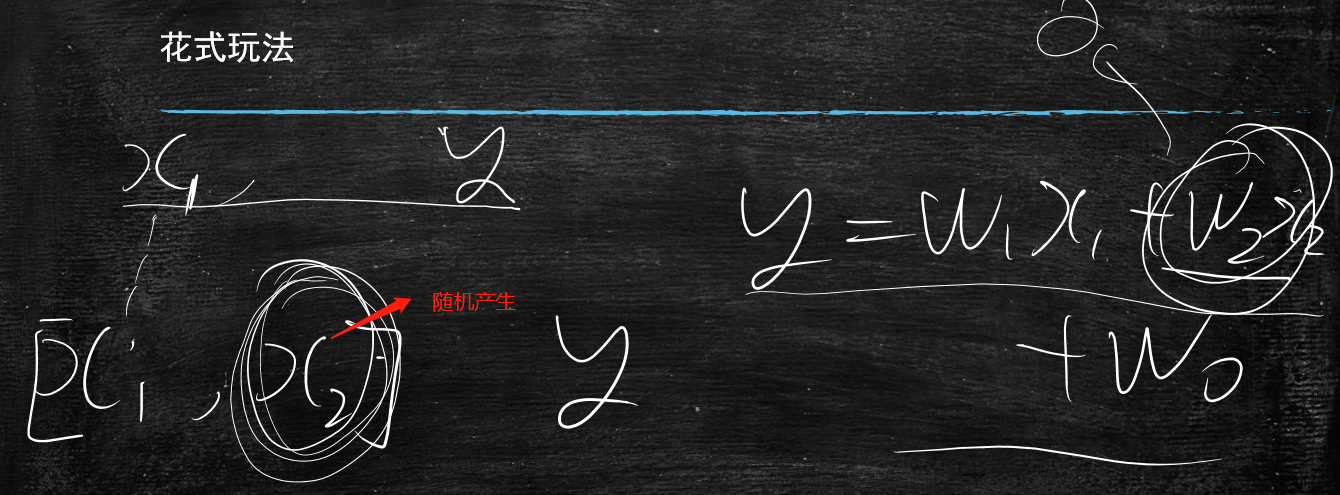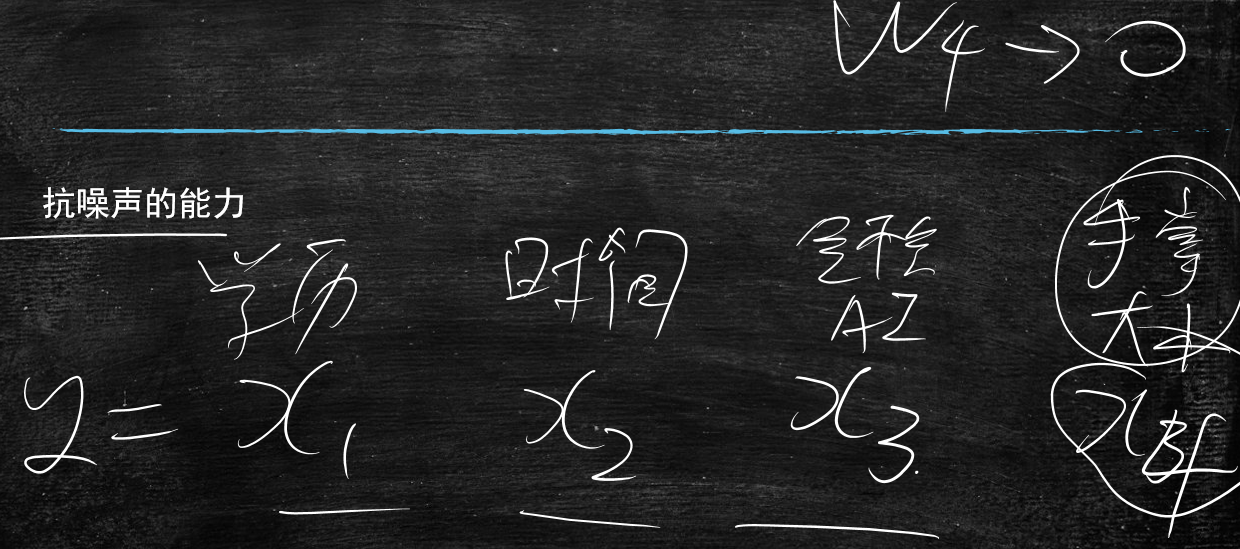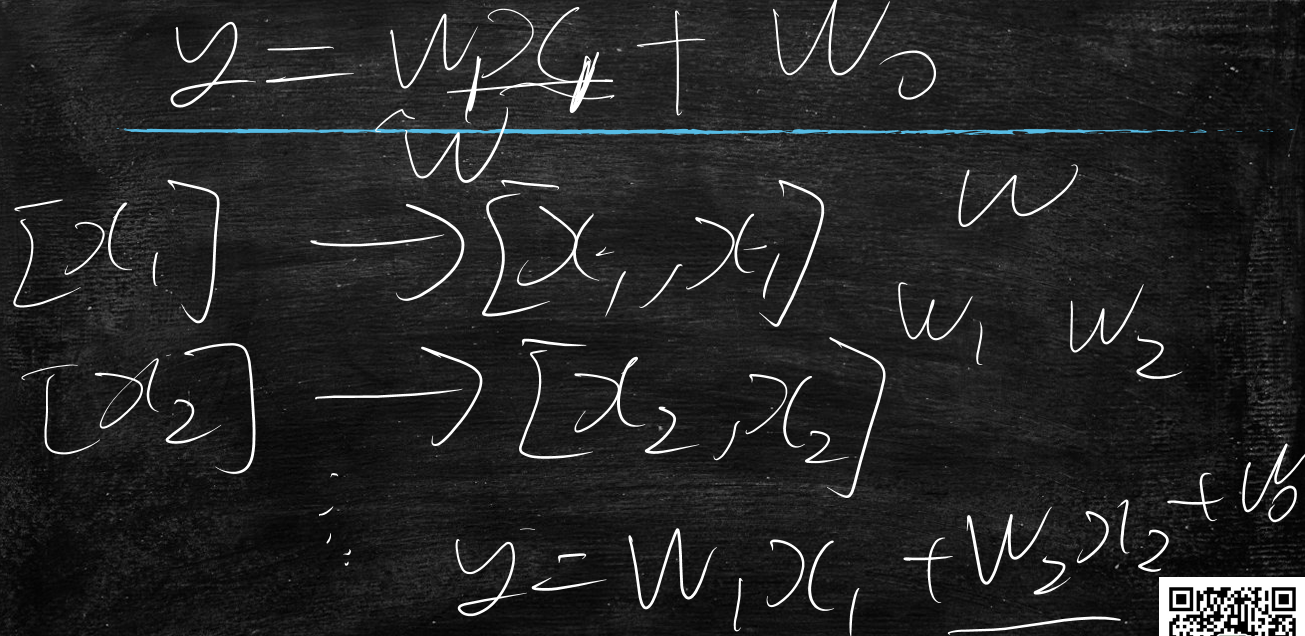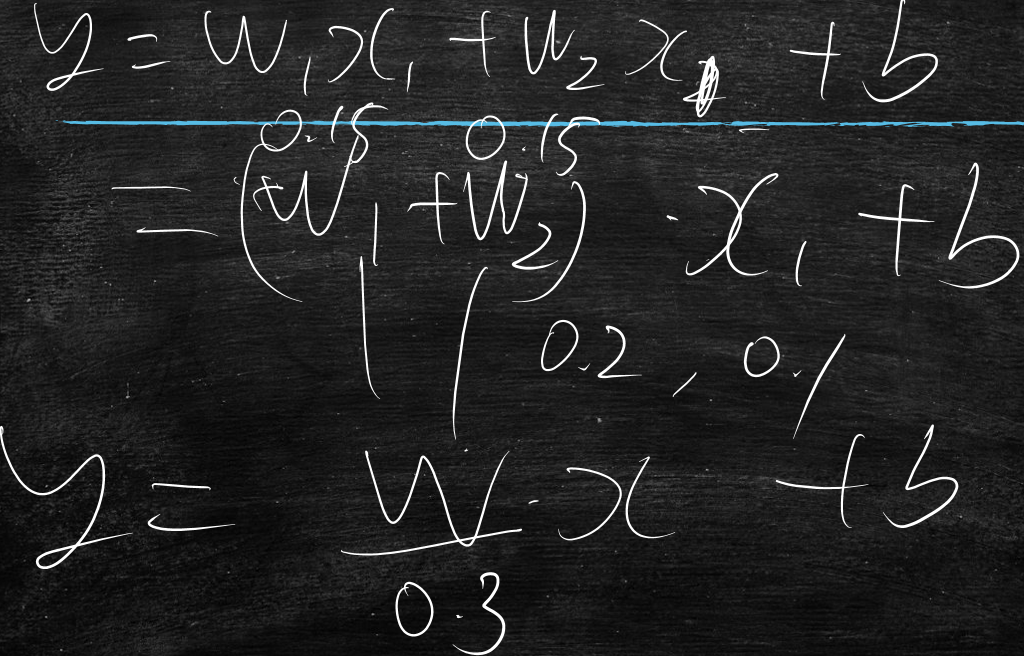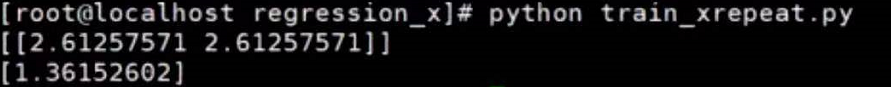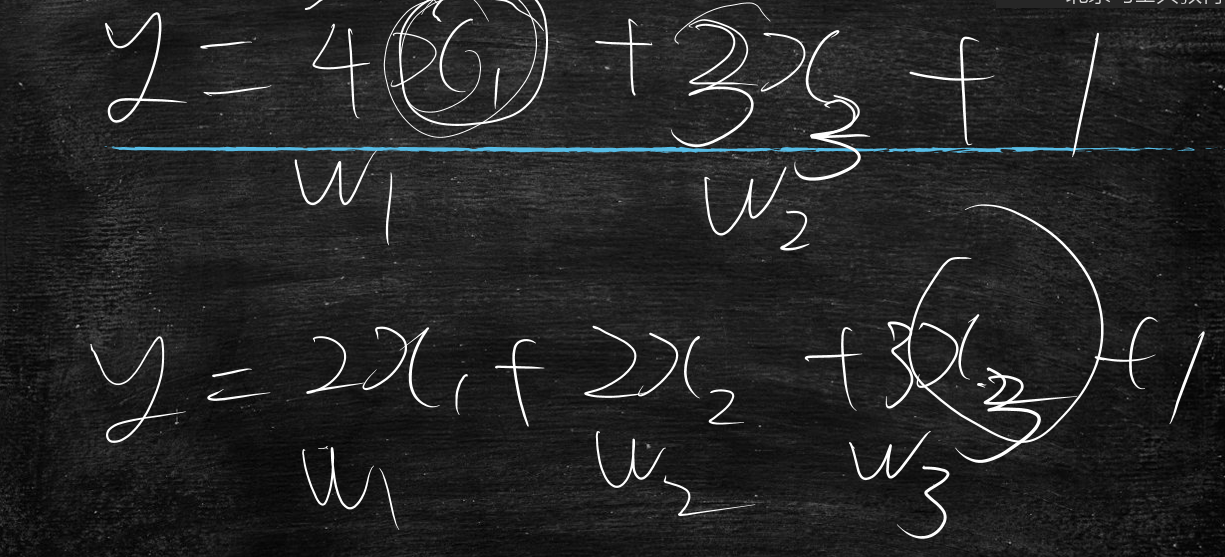ShiYu

# 突破瓶颈，模型效果的提升

再次回顾下，方差与绝对值的问题

image-20220309150846063

平方：开始会找那些好弄的点，但是后面会照顾下那些不好弄的点

绝对值：不会这样，只集中在好弄的点上

好弄的点：在主直线上，或者离着主直线很近的点

不好弄的点：不在主直线上，而且离主直线还很远的点

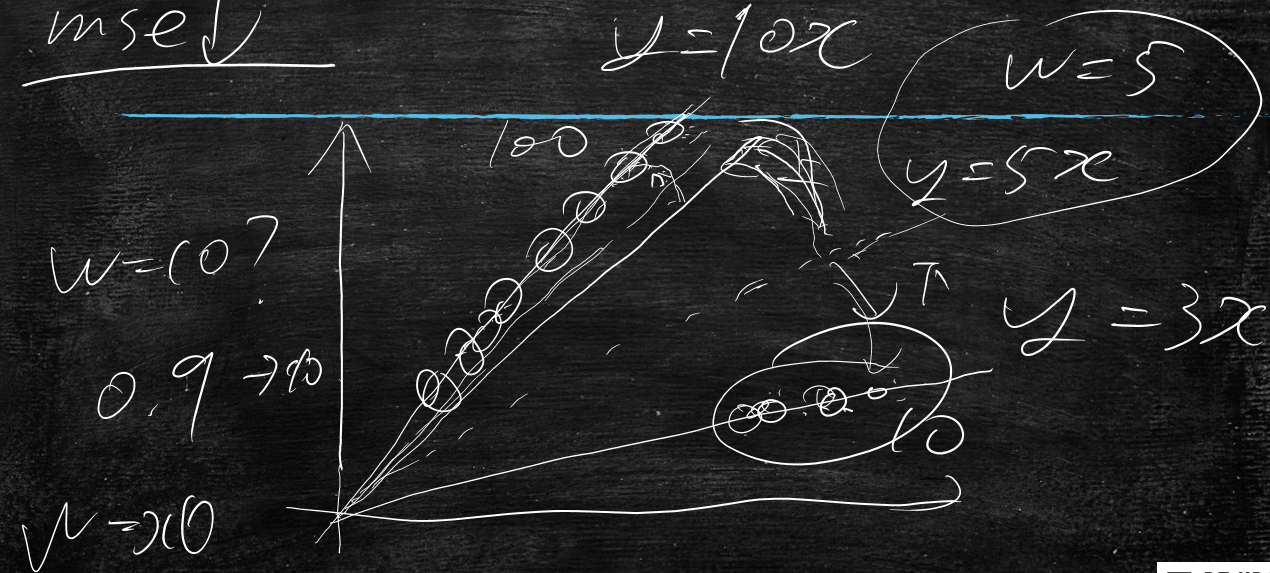
比如，有条直线(y=10x)覆盖着100个点，有条直线(y=3x)覆盖着10个点

那么从全局上看y=10x上面的点是好弄的点，y=3x是不好弄的点

使用平方时：初始时，w=5，y=5x，w会逐渐变大，但是不会走到10的，当快到10后，会逐渐变小，照顾到y=3x这些点

使用绝对值时：它会走到y=10x，w不会变小了，照顾不到y=3x这些点了

所以采用平方

image-20220309151533050

下面通过实际手写代码对比使用平方训练及使用绝对值训练的区别

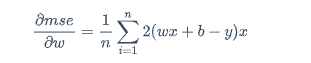
使用平方的公式： $$ \frac{\partial mse}{\partial w}=\frac{1}{n}\sum_{i=1}^{n}2(wx+b-y)x $$ image-20220309144829044

使用绝对值的公式：

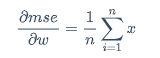
当wx+b-y>0时 $$ \frac{\partial mse}{\partial w}=\frac{1}{n}\sum_{i=1}^{n}x $$ image-20220309153844822

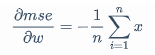
当wx+b-y<0时 $$ \frac{\partial mse}{\partial w}=-\frac{1}{n}\sum_{i=1}^{n}x $$ image-20220309153853556

当wx+b-y=0时，随机取上面两值中的一个

手写实现对比代码

gradient_linear.py

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys) 
sys.setdefaultencoding('utf-8') 
import random
def get_data(w,num):
	x=[ random.uniform(0,5) for  i in range(0,num)]
	y=[ w*s for s in x]
	return zip(x,y)
def train_step_pow(data,w,rate=0.03):
	g=sum([ (w*x-y)*x  for [x,y] in data])/len(data)
	w=w-rate*g
	return w
def train_step_abs(data,w,rate=0.03):
	g=sum([ x if  (w*x-y)>0 else -1*x  for [x,y] in data])/len(data)
	w=w-rate*g
	return w
	
def cal_data_error(data,w):
	error=[(w*x-y)*(w*x-y)  for [x,y] in data ]
	return error


#第一个参数是w 第二个参数是数量
data=get_data(10,10) +get_data(6,2)
w1=w2=7
#pre_errors=cal_data_error(data,w)
for i in range(0,5000):
	w1=train_step_pow(data,w1)#正规mse训练
	w2=train_step_abs(data,w2)#绝对值mse训练
	if i%50==0:
		#errors=cal_data_error(data,w)
		#mse_delta=[ "%.3f"%(e2-e1) for [e1,e2] in zip(errors,pre_errors)]
		#pre_errors=errors
		print "{},{}".format(w1,w2)
		#print " ".join(mse_delta)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

执行结果

image-20220309154240013

平方计算出的w1不会到10的

绝对值计算出的w2会无限接近于10

多元线性回归

线性回归中是：y=wx+b，这里面的x是一个维度

但是现实世界中是有多个维度构成，比如预测房价

地段是x1，

当地的经济水平是x2，

人口密度是x3

。。。。。。

最终预测房价y

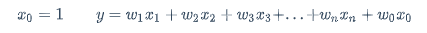
真实世界中变量是多元的，那么就是使用多元线性回归 $$ x_0=1 \qquad y=w_1x_1+w_2x_2+w_3x_3+...+w_nx_n+w_0x_0 $$ image-20220309163130711

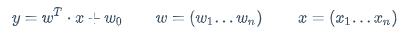
可以简写为： $$ y=w^T \cdot x+w_0 \qquad w=\left(w_1...w_n\right) \qquad x=\left(x_1...x_n\right) $$ image-20220309163959917

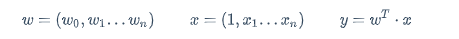
更简写为： $$ w=\left(w_0,w_1...w_n\right) \qquad x=\left(1,x_1...x_n\right) \qquad y=w^T \cdot x $$ image-20220309164010496

多元线性回归代码示例

train.py

# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict
from numpy import shape
from sklearn import metrics
import numpy as np
def extend_feature(x):
	result=[x[0],x[0]]
	result.extend(x[1:])
	return result
	#return [x[0],x[0]]
def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=[extend_feature(x) for x in X]
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
 
 
model = LinearRegression()
model.fit(X_train, y_train)
 
print (model.coef_)#打印w
print (model.intercept_)#打印w0 就是b
 
y_pred = model.predict(X_train)
print "MSE:", metrics.mean_squared_error(y_train, y_pred)

y_pred = model.predict(X_test)
print "MSE:", metrics.mean_squared_error(y_test, y_pred)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

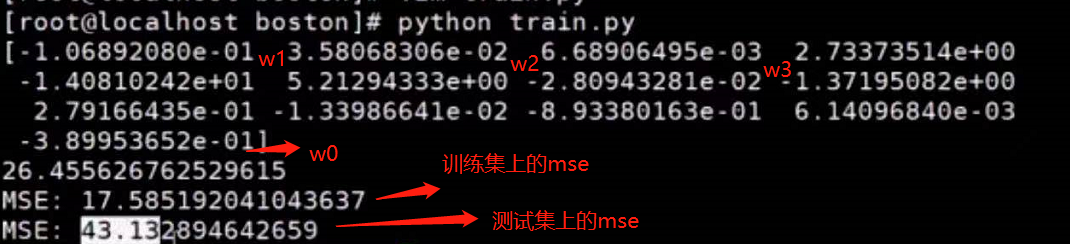
执行结果

image-20220309164533866

image-20220309163130711

在多元变量中，当w1越大说明x1对y值的影响就大

当w1=0，那么x1怎么变都不影响y值

当w1>0，那么x1对y值就是正影响

当w1<0，那么x1对y值就是负影响

说明通过这些权重(w)看出哪些元(x)的重要程度

扩展一下

使用线性回归的前提条件：数据尽量在一条直线上

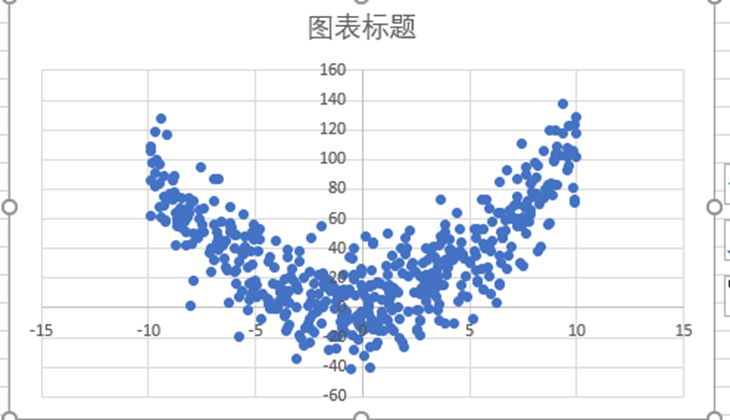
比如下图是我的原始数据是这样(类抛物线)的，那么用线性回归模型怎么搞呢？

image-20220309165251803

这样的数据先天就不在一条直线上，使用直线拟合天然不好，所以要使用抛物线拟合

那么抛物线的方程式为： $$ y=ax^2+bx+c $$ image-20220309165715397

那么用线性回归怎么搞呢？

从一元变为二元 $$ y=w_1x^2+w_2x+w_0 $$ 将x的平方单独看成一项，这样学出来是条抛物线，那么还是线性回归吗？这里先留个悬念

先看个将线性回归改变为抛物线代码示例

主要是对x进行了变换，就是将原来的[x[0]]变为[x[0],x[0]*x[0]]

多了一项为自己的平方

train_xsquare.py

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys) 
sys.setdefaultencoding('utf-8') 
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import metrics
def extend_feature(x):
	#return [x[0]]
	#x=[2]
	#x=[2,4]
	return [x[0],x[0]*x[0]]

def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=[ extend_feature(x) for x in X]
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_paracurve_data")
X_test,y_test=read_data("test_paracurve_data")
model = LinearRegression()
model.fit(X_train, y_train)
print model.coef_
print model.intercept_


'''
y_pred_train = model.predict(X_train)
train_mse=metrics.mean_squared_error(y_train, y_pred_train)
print "特征+平方非线性"
print "MSE:", train_mse
y_pred_test = model.predict(X_test)
test_mse=metrics.mean_squared_error(y_test, y_pred_test)
print "MSE:",test_mse
print "推广mse差", test_mse-train_mse
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

执行结果

image-20220309170549510

那么得出的方程式为： $$ y=0.93645083x+0.99678729x^2+3.107421 $$ image-20220309170740174

这样就能拟合抛物线了

思考

方程式1： $$ y=w_1x+w_0 $$ image-20220309171520141

方程式2： $$ y=w_1x+w_2x^2+w_0 $$ image-20220309172134847

在训练集上，方程式2得到的结果有没有可能会比方程式1得到的结果要差呢？

答：是不可能的，如果w2=0时，那么方程式2就会退化为方程式1

所以说在训练集上项式就往上加，学习的结果至少不会变差的

再次扩展

当我们的曲线越来越复杂时，如下图

image-20220309170942456

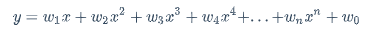
那么此时就是平方不够再上立方，再上4次方等等，就是我的多项式不断的往上加，曲线会越来越复杂 $$ y=w_1x+w_2x^2+w_3x^3+w_4x^4+...+w_nx^n+w_0 $$ image-20220309171153005

由于不断的往上加，会导致数学上的噩梦==>>泰勒公式

任意函数都可以分解为 $$ n \rightarrow \infty \qquad y=w_1x+w_2x^2+w_3x^3+w_4x^4+...+w_nx^n+w_0 $$ 如果不考虑计算成本的话，不管数据图长成什么样，都能通过泰勒公式完美的拟合出来

image-20220309172119034

所以说这个公式还是非常牛的啊，能搞定任意函数

刚才说使用多项式在训练集上效果很好，但是在测试集上效果未必好了

那么来分析一下为什么会这样呢？

如果全量数据是条主直线

正常拿到的数据会偏离主直线，大致会在主直线附近震荡

当在训练集上使用多项式公式当n很大时，它会过所有的点，学习一条诡异的曲线，mse都可以趋近于0了，把噪声都学会了

这是在测试集上使用训练集的模型时，mse会变大，偏离这条主直线

image-20220309173250165

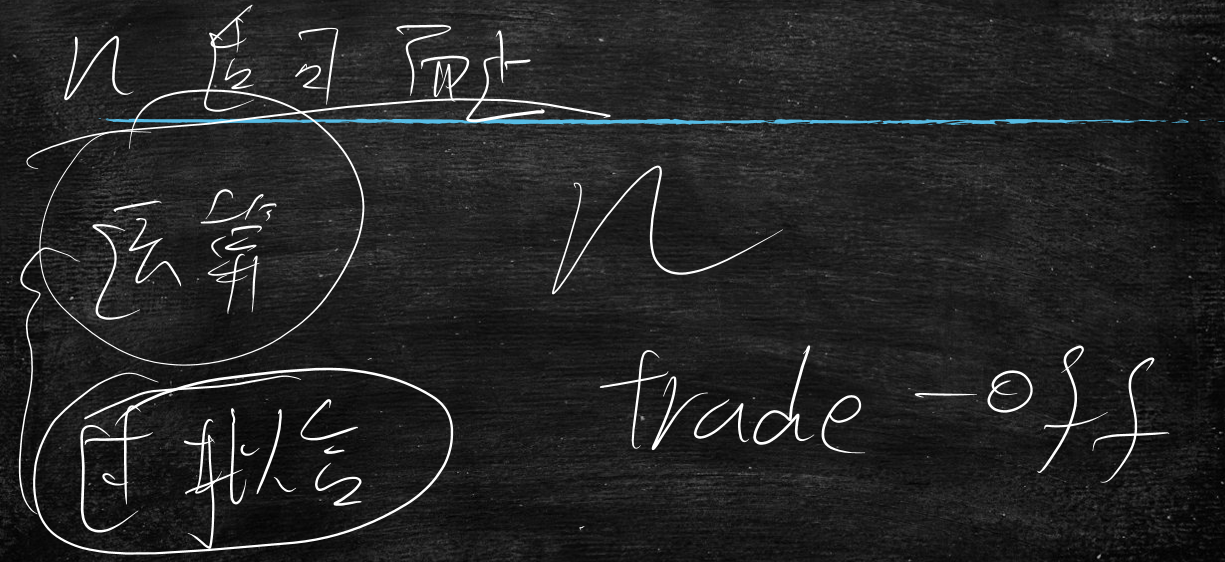
所以在实际工程中，n的取值要适可而止

会产生如下问题

  • 运算量过大
  • 过拟合

image-20220309174304263

所以这个n也是个调参点

线性回归的花式玩法-抗噪声

向量是一个x1，输出一个y

然后加一个向量[x1,x2]，输出一个y

但是x2是随机产生(random.uniform(-10,10))，y=w1x1+w2x2+w0

那么我训练出来的w2是多少呢？

image-20220309175053999

示例代码

train_xrandom.py

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys) 
sys.setdefaultencoding('utf-8') 
import numpy as np
import random
from sklearn.linear_model import LinearRegression
from sklearn import metrics
def extend_feature(x):
	return [x[0],random.uniform(-10,10)]

def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=[ extend_feature(x) for x in X]
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
model = LinearRegression()
model.fit(X_train, y_train)
print model.coef_
print model.intercept_


'''
y_pred_train = model.predict(X_train)
train_mse=metrics.mean_squared_error(y_train, y_pred_train)
print "+随机特征"
print "MSE:", train_mse
y_pred_test = model.predict(X_test)
test_mse=metrics.mean_squared_error(y_test, y_pred_test)
print "MSE:",test_mse
print "推广mse差", test_mse-train_mse
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

执行结果

image-20220309175454627

w2趋近于0

说明线性回归有抗噪声能力，它会排除那些跟目标完全没有关系的那项

比如说预测一个人拿多少薪水，跟他的手掌大小是没有任何关系的

x1是学历

x2是工作时间

x3是是否会AI

x4是手掌大小

唯独w4是趋近于0的

学了无关的项式，最多牺牲了运算量，但是模型不至于很差

image-20220309175857470

线性回归的花式玩法-抗冗余

y=wx1+w0

向量重复一下

将特征向量[x1]变为[x1,x1]

将特征向量[x2]变为[x2,x2]

方程式变为y=w1x1+w2x2+w0

那么w与w1、w2有什么关系吗？

image-20220309180624983

image-20220309180639726

代码示例

train_xrepeat.py

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import sys
reload(sys) 
sys.setdefaultencoding('utf-8') 
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import metrics
def extend_feature(x):
	return x
	#return [x[0],x[0]]

def read_data(path):
	with open(path) as f :
		lines=f.readlines()
	lines=[eval(line.strip()) for line in lines]
	X,y=zip(*lines)
	X=[ extend_feature(x) for x in X]
	X=np.array(X)
	y=np.array(y)
	return X,y
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
model = LinearRegression()
model.fit(X_train, y_train)
print model.coef_
print model.intercept_


'''
y_pred_train = model.predict(X_train)
train_mse=metrics.mean_squared_error(y_train, y_pred_train)
print "特征+平方非线性"
print "MSE:", train_mse
y_pred_test = model.predict(X_test)
test_mse=metrics.mean_squared_error(y_test, y_pred_test)
print "MSE:",test_mse
print "推广mse差", test_mse-train_mse
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

执行结果

image-20220309181032376

image-20220309181151217

w=w1+w2

会出现一种巧妙的情况

y=w1x1+w2x2+w3x3+w0

y是交往女朋友的数量

x1是身高

x2是体重

身高与体重冗余的程度很高的，因为一般知道了身高，那么其体重八九不离十的估算出来的，虽然不是纯冗余，但是高度相关

那么再加入x3是收入，收入与身高和体重就相关不大了

线性回归的优点：加入纯噪声对mse没有任何伤害，加入纯冗余对mse没有任何帮助，降低特征提取难度

加入冗余后，w就不能代表权重了

image-20220309182238437

上图所示，之前是x1最重要，下面则变为x3最重要了

正因为存在着冗余，那么w不能当做权重来看

所以只有在线性无关，没有冗余的前提下，w才代表权重

虽然线性回归是最简单的模型，但是它是逻辑回归的基础，逻辑回归又是现在最流行的深度学习的基础

所以理解线性回归的理论很重要

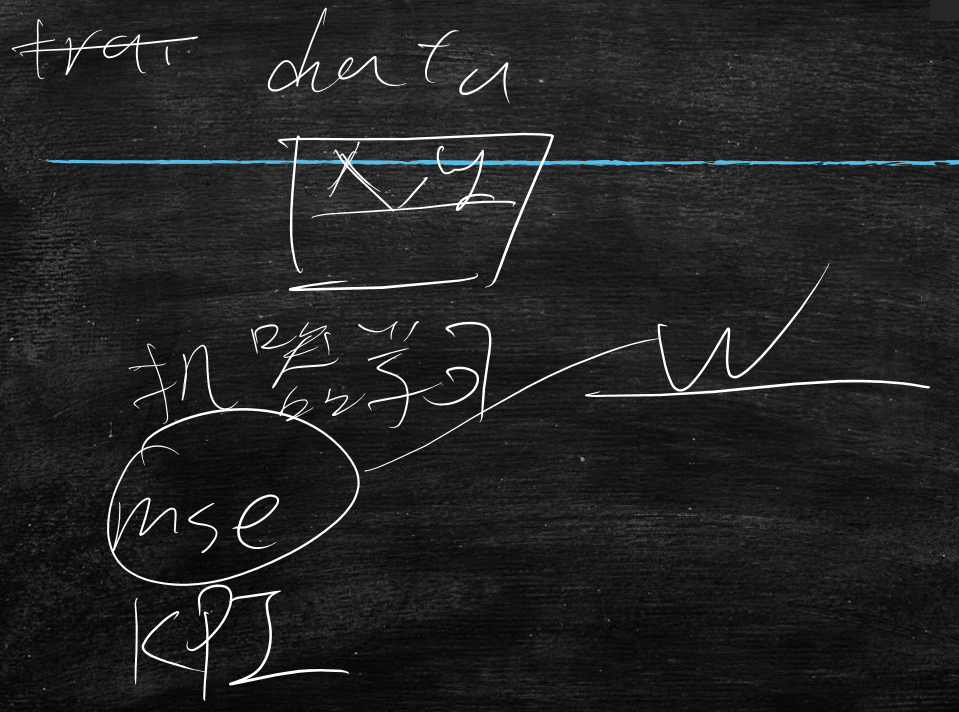
总结-机器学习的套路

  • 首先准备数据(一般是大数据data，数据量越大越好)，告诉机器学什么东西(就是w)，目标为mse、KPI，通过mse来引导这个w该如何的改变，这时就是方差与绝对值两种导致w的不同

    image-20220309183539654

  • 整个机器学习就是一个工具箱，学习的线性回归是工具箱里的一个螺丝刀，它里面还有钳子、扳手等很多工具，将这些工具掌握以后，在业务场景中，挑选工具来用

    image-20220309183718608

作业

结合目前所在公司的业务，找出机器学习可以用到的点，用学习到的AI知识去实现它

例如：

在餐厅里

x可以是菜品销量、蔬菜价格、季节等等

y可以是明天该近多少斤茄子

image-20220309184631686

在广告公司里

有两个特征

第一个特征是广告的领域、卖的东西、价格等等

第二个特征是用户的搜索词、用户画像

y是0~1范围的值，0代表用户不会点击该广告，1代表用户会点击该广告

image-20220309184958441

y=0.9用户选择广告2的概率会高

image-20220309185014938

又比如广告有100个标签，那么向量x就是100维

当广告中出现某个标签时，该位置写1，反之写0，这就是特征了

image-20220309190228137

讲完线性回归，其实整个机器学习的套路已经讲完70%了，剩下的30%新内容，用各种形式不断的重复70%，不断的加深理解

AI很大程度上解放人力

题外话

机器学习的理论基石，是几百年前，下面4位大佬奠定的

  • 牛顿-莱布尼茨
  • 泰勒
  • 贝叶斯
  • 高斯

所以说学了机器学习后，就会深感他们四位的厉害之处，在没有计算机的时代，奠定了机器学习的基础

领先世界几百年，也说明了几百年没有进步了

← 猛将起于卒伍，工业环境下的分类模型 →