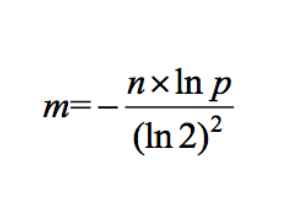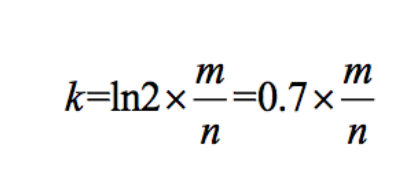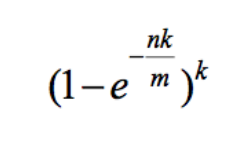# 第33节 与哈希函数有关的结构
# 哈希函数
概念:
常见哈希算法:
- SHA-1,SHA-256,SHA-512
- MD5
特点:经典哈希函数
- 输入:输入域无限大,例如:任意长度的字符串
- 输出:输出域相对有限的,0~2^64-1、0~2^128-1,一般是数字或者字节数组
- 特征:它不具有随机性,相同的输入绝对是返回相同的输出,那么就会有这样的问题:输入域是无限的,输出域相对有限,这样必然会哈希碰撞,就是不同的输入可能会返回相同的输出
- 重要特征:如果把输出域想象为坐标系的x轴,这时有大量的不同输入进来,映射到x轴的不同的点上,这时拿一个长度固定的尺子,不管尺子放在x轴的哪个位置,尺子压到的点的数量是差不多的,就是说大量的不同输入,它会离散的散落在x轴上,这就是它的离散性(均匀性),能够保证均匀分布;一种形象的比喻:认为整个输出域是一个密闭的房间,有一瓶香水,里面放着不同的输入,然后将香水打碎后,哈希函数会把每一个香水分子带到房间的某个位置,导致的效果是房间的随机一个位置,香水浓度都差不多
- 由于哈希函数的输出是均匀分布的,例如在0~2^128-1上均匀分布,如果%10则在0~9上均匀分布
- 作用:可以把数据根据不同值,几乎均匀的分开
代码演示:
package class33;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
import java.security.Security;
import javax.xml.bind.DatatypeConverter;
public class Hash {
private MessageDigest hash;
public Hash(String algorithm) {
try {
hash = MessageDigest.getInstance(algorithm);
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
}
public String hashCode(String input) {
return DatatypeConverter.printHexBinary(hash.digest(input.getBytes())).toUpperCase();
}
public static void main(String[] args) {
System.out.println("支持的算法 : ");
for (String str : Security.getAlgorithms("MessageDigest")) {
System.out.println(str);
}
System.out.println("=======");
String algorithm = "MD5";
Hash hash = new Hash(algorithm);
String input1 = "zuochengyunzuochengyun1";
String input2 = "zuochengyunzuochengyun2";
String input3 = "zuochengyunzuochengyun3";
String input4 = "zuochengyunzuochengyun4";
String input5 = "zuochengyunzuochengyun5";
System.out.println(hash.hashCode(input1));
System.out.println(hash.hashCode(input2));
System.out.println(hash.hashCode(input3));
System.out.println(hash.hashCode(input4));
System.out.println(hash.hashCode(input5));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
哈希函数的实际例子
哈希表的设计:为什么增删改都是O(1)?这么逆天的复杂度
假设
Map<String,Integer>,过程分为入桶与桶扩容
- 入桶:哈希表有个初始的桶区域,设置桶长度为17,假设来了一个键值对数据(
abc,25),先将abc通过哈希函数算出个哈希值f(abc),然后%17,得出数值一定在0~16上,假设这个值为5,那么就将键值对数据(abc,25)挂在5号桶里,桶里怎么连接数据,采用单链表数据结构,假设又来了一个键值对数据(bk,17)经历了上面的哈希函数再%17,假设得出数值为9,那么就将键值对数据(bk,17)挂在9号桶里,假设又来了一个键值对数据(se,34)经历了上面的哈希函数再%17,假设得出数值为5,那么5号桶里有数据了,那么就顺着数据往下挂,单链表上挂数据,因为哈希函数具有均匀性,所以当加入很多不同的key后,0~16号桶里的数据一定均匀增长,查找:假设查找键值对数据(bk,17),根据bk经历哈希函数再%17算出在9号桶,然后遍历桶里的链表得到键值对数据(bk,17),但是这个有问题:桶长度为17,我有N个数据,那么每个桶里大概是N/17条数据,那个查找的代价就是O(N/17)->O(N),针对这个问题,于是有了桶扩容操作- 桶扩容:针对上面问题,于是出现这样的规则:当桶的链长度超过6到达7时,就会发生桶扩容,扩容一倍,也就是17->34,桶中数据重新经历哈希函数再%34,入桶操作,经过扩容每个桶的链长度差不多是原来的一半,然后再当桶的链长度超过6到达7时,再次扩容,周而复始
- 证明增删改都是O(1):假设哈希表按照最差情况,设定初始桶长度为1,桶的链长度到达2就要扩容,假设已经加到1000条数据了,那么在这个加入过程中触发了几次扩容操作?当第1个数据来到的时候,入桶O(1),当第2个数据来到的时候,扩容,挂在长度为2的桶里,扩容代价为O(2),当第3个数据来到的时候,扩容,挂在长度为4的桶里,扩容代价为O(3),当第5个数据来到的时候,扩容,挂在长度为8的桶里,扩容代价为O(5),当第9个数据来到的时候,扩容,挂在长度为16的桶里,扩容代价为O(9),通过上面列举会发现规律,扩容总代价为O(1)+O(2)+O(3)+O(5)+O(9)+O(17)+O(33),下一次是上一次的两倍,等比数列,得出结论,当加入N个数据,扩容次数为logN次,又由于总的扩容代价是等比数列趋近于O(2n),去掉常数项,所以O(N),平均一次的代价为O(N/N) ->O(1)
- 工程上优化常数时间:初始桶长度设置,桶放入红黑树结构,优化常熟时间,对于时间复杂度没有改变都是O(1)
# 布隆过滤器
- 利用哈希函数的性质
- 每一条数据提取特征
- 加入描黑库(bitmap位图)
布隆过滤器现在大量被工程上使用,例如Redis中防止穿透等
布隆过滤器:在允许一定失误率的情况下,实现类黑名单的功能
功能要求:
假设我有个大集合(Set)存放大量的字符串url,比如说100E个url,每个url大小不会超过64Byte,将大集合变为服务,就是以后出现个url就在集合中查询一下是否包含,类黑名单的功能,若url在集合中就不给用户显示,若不在则显示给用户。
最简单的实现:
将url存入HashSet中,但是就想完整存下,至少需要64*100E 个Byte=>640G内存容量,考虑到成本问题,一般工程实现上要做出一定的妥协,于是布隆过滤器就登场了。
布隆过滤器实现:
在允许一定失误率的情况下(0.1%万分之1),实现功能,但是大大的减少所需的空间,大概只占用18多G内存容量,缩小容量将近32倍,一定会有失误率,但是可以控制在一定的范围内,而且这个失误率是url是在集合中的这种不会有失误,失误的是不在集合中的url可能会误判定为在集合中,属于宁可错杀三千,不能放过一个的类型。
举个例子:
在搜索引擎来说,有自己爬虫程序,可能有1000个程序同时在爬取网页,假如爬虫1程序爬取了一个url,不希望别的999个爬虫程序再重复爬取这个url,所以当爬虫1程序爬取了一个url就要加入这个黑名单服务中的大集合中,别的爬虫程序再运行爬取逻辑前先去验证url是否存在,再做决策,存在直接跳下一个url,不存在我再爬取url。
布隆过滤器设计原理:
首先要了解什么是位图(bitmap)? 补下常识
现在我有个int[10]的数组,0位置上是int类型数据占用空间4Byte,1位置上是int类型数据占用空间4Byte
所以长度10的int数组,占用空间40B,那么假设是个bit[]的数组,0位置是一个bit,1位置也是一个bit,那么假设这个bit[]数组有n长度,那么它占用空间(n/8)B,因为1B=8bit
说回到int[10]的数组,0位置上是int类型数据占用32bit(位),那么int[10]就相当于bit[320]
布隆过滤器可以理解为它是一部分逻辑加上位图的一个整体:
假设准备一个长度为m的bit[m]数组,占用空间(m/8)Byte,这个数组可以理解为是布隆过滤器的物理结构;
假设准备了三个哈希函数分别是f1(),f2(),f3(),每一个url->str1要添加到集合中经历如下过程:
str1经历哈希函数f1算出哈希值C1,然后%m->得到的数值x,在位图bit[m]数组找到这个数值x的位置设置为1(描黑);str1经历哈希函数f2算出哈希值C2,然后%m->得到的数值y,在位图bit[m]数组找到这个数值y的位置设置为1(描黑);str1经历哈希函数f3算出哈希值C3,然后%m->得到的数值z,在位图bit[m]数组找到这个数值z的位置设置为1(描黑);周而复始一直到100E个url在位图上描黑。
url验证存在逻辑:有个url->str通过三个哈希函数然后再%m,算出三个位置数,在位图上查看,若有一个位置不为黑,则说明url不在集合中,若是三个位置都黑了,则说明url在集合中;
以上就是布隆过滤器的设计原理,那么问题关键就是m定多大?哈希函数个数k定多少个?
如果m太小则位图会很快全黑,接下来查询哪个url都在集合中->失误率太大了
如果m太大则存在浪费空间的问题。
当样本量(n)与空间(m)固定,m与失误率(p)关系为m越大则失误率(p)越小趋近于0,但是永不为0
布隆过滤器要开多大(m)的决定因素有哪些?
- 样本量->100E(有关)
- 失误率->0.01%(有关)
- 单个样本大小->64B(无关)
哈希函数个数k的决定因素有哪些?
- 样本量->100E(有关)
- 布隆过滤器要开多大(m)(有关)
如果哈希函数个数太少比如就1个则会产生采样不足,很容易碰撞,失误率变大
如果哈希函数个数太多比如就1千万个那么一个url会描黑1千万个位信息,m可用的范围下降,失误率变大
当样本量(n)与空间(m)固定,k一开始越大则失误率(p)越小,后面k越大则失误率(p)越大
布隆过滤器重要的三个公式
1,假设数据量为n,预期的失误率为p(布隆过滤器大小和每个样本的大小无关) 2,根据n和p,算出Bloom Filter一共需要多少个bit位,向上取整,记为m
3,根据m和n,算出Bloom Filter需要多少个哈希函数,向上取整,记为k
4,根据修正公式,算出真实的失误率p_true,若是m_true比m大的话,p_true一定小于p
整个过程梳理:
现有条件:样本量n=100E,失误率p=0.01%(万分之一)
1、根据n和p,算出Bloom Filter一共需要多少个bit位,向上取整,记为m,算出的是bit,(m/8)Byte假设是17G
那么这时就提出问题:现在满足现有失误率的情况下,布隆过滤器需要至少17G的空间,是否能多给点空间,比如申请20G,我就能将失误率p降的更少,若是可以,则现在就有了两个m值,一个是至少m1,另一个是实际拿到的m2
2、根据m2和n,算出Bloom Filter需要多少个哈希函数,向上取整,记为k,k = m2/n*0.7 = 12.7向上取整k2=13个,其中k=12.7是理论值,k2=13是实际值
13个哈希函数怎么制造?
只需要两个哈希函数f1、f2 线性的制造任意个哈希函数 每个哈希函数几乎独立
第一个哈希函数=>1*f1+f2
第二个哈希函数=> 2*f1+f2
...
第n个哈希函数=> = n*f1+f2
3、根据m2和k2,拿到的实际值,算出真实的失误率p_true,
若是m_true比m大的话,p_true一定小于p=0.01%(万分之一)
布隆过滤器的妙用:
在HDFS存储集群中,假如有三个分片分别定义为c1、c2、c3;这时候要查找“abc”,若是没有布隆过滤器,那么只能MapReduce,并行去查找,若是有布隆过滤器,通过布隆过滤器得知c1上有"abc",则直接在c1中查找即可
# 一致性哈希环
分布式存储结构最常见的结构
1)哈希域变成环的设计
2)虚拟节点技术
一致性哈希解决的是数据存储问题:
假设有个键值对数据("杨", 35)想要存入数据库,请求->前端层->逻辑端层->数据端(MySQL)
假设数据端服务器有三台分别是0、1、2号机器,那么我怎么确定这个键值对数据("杨", 35)归于哪个机器上?
一种经典的方法是:"杨"通过哈希函数得出一个数值c1,再%3,假设结果是0,那么键值对数据("杨", 35)存在0号机器,最多给0号机器来个从机;又来个键值对数据("超", 37),"超"通过哈希函数得出一个数值c2,再%3,假设结果是1,那么键值对数据("超", 37)存在1号机器;根据哈希函数的均匀性,数据会均匀分散到这三台机器上,我们把"杨"、"超"这样的key,在业务上叫做HashKey(专门均匀分配的),但是如果HashKey选择的不当,可能会出现严重的问题,比如把国家名称(中、俄、美)搞成了HashKey,这样虽然key是均分了,但是来自中、俄的用户访问很多,但是总有一台机器是不处理来自中、俄的用户访问的,造成资源的浪费,负载不均衡,就是业务上少量国家有高频,这种时候会带来负载不均衡。那么就要分析高频的key有哪些?中频的key有哪些?低频的key有哪些?这些都要通过具体的业务来挖掘适合做HashKey的,来实现负载均衡。其实这套方法很完美了,只要选好HashKey,那么这三台机器会特别均衡。但是有个问题,请看下面。带来的问题是:扩容不便,增加一台机器,所有数据会%4,迁移数据的代价是全量的
一致性哈希:就是迁移数据的代价不是全量的前提下,还能够做到负载均衡。
设计原理(不需要取模):
哈希域变成环的设计:1)把哈希函数的返回域的值(0~2^64-1),想象为一个环,唯一的哈希函数f1
2)假设一开始有三台机器分别为m1、m2、m3,机器中有不同的ip、hostname、mac等信息,假设选定ip,那么每个机器的ip就是个字符串,ip1经历哈希函数f1->c1,ip2经历哈希函数f1->c2,ip3经历哈希函数f1->c3,
将c1、c2、c3上哈希环,环上就有c1、c2、c3这三个位置,上环的作用:现在一个信息来了,假设键值对数据("杨", 35),"杨"通过哈希函数得出一个数值d4,上环,假设d4在c1与c2之间,d4归属于顺时针遇到的第一台机器就是c2,可以理解为有序数组中(从小到大)比d4大的最左的数c2;
3)如果加入一台机器m4,它会将ip4经历哈希函数f1->c4,上环,假设c4在c1与c3之间,那么c3~c4这段原本是m1机器存储的数据要迁移至m4机器,迁移代价很少;同样的我要下线m4,c4顺时针找到第一台机器m1,将m4机器的数据都迁移给m1机器,完成下线操作
带入具体数值感受一下:
假设三台机器分别为m1、m2、m3,那么每个机器的ip就是个字符串,ip1经历哈希函数f1->7,ip2经历哈希函数f1->64,ip3经历哈希函数f1->9,将这三个值排序,得到一个路由表[7=m1,9=m3,64=m2];那么前端层还是之前的,逻辑层的机器中每一个会得到这个路由表[7=m1,9=m3,64=m2],当键值对数据("杨", 35)到达后,"杨"通过哈希函数得出56,怎么顺时针找?相当于在有序数组中>56的最左位置的数m3,那么该数据归属m3机器,而且有序数组中找到大于某个数最左的数过程是可以二分的,哪怕是几千几万台机器,也很快就能定位,速度很快。
问题1:有三台机器,怎么保证三台机器能够均分?(这个与哈希函数的均匀性不是一回事),可能一上环就不均分。
问题2:哪怕是人为分配三台机器,三个哈希值,能够均分,但是扩容呢?增加一个机器进去,立马不均了
为了解决上述两个问题带来了虚拟节点技术:1)还是有三台机器分别为m1、m2、m3,但是这次是给m1分配1000个字符串(a1.....a1000),给m2分配1000个字符串(b1.....b1000),给m3分配1000个字符串(c1.....c1000),这是个路由表,每台机器有哪些字符串是可以查到的,哪些字符串归属于哪个机器也可以查到,m1有1000个虚拟节点,m2有1000个虚拟节点,m3有1000个虚拟节点,它们直接互相查很方便,
2)让m1的1000个虚拟节点,帮m1上环,m2、m3的1000个虚拟节点也是这样,虚拟节点(a1.....a1000)占据的实际位置是属于m1的,虚拟节点(b1.....b1000)占据的实际位置是属于m2的,虚拟节点(c1.....c1000)占据的实际位置是属于m3的,由于哈希函数的均匀性,这些虚拟节点几乎均匀分布在环上,这样就实现了三台机器的数据均衡,打个比喻,输出域是一间房,有三种香水A、B、C,将三种香水打碎,房间的每一个位置三种香水的浓度几乎一样。
3)如果加入一台机器m4,给m4分配1000个字符串(d1.....d1000),m4的1000个虚拟节点,帮m4上环,由于哈希函数的均匀性,m4的1000个虚拟节点会均匀的分布,那么m4的1000个虚拟节点会均等向m1,m2,m3所控制的虚拟节点要数据,每个机器要1/12数据,要来三份就是3/12->1/4,这样又实现了均分。迁移的代价是m1的全量的1/12+m2的全量的1/12+m3的全量的1/12,即是总量的1/4
举个例子:首先三个机器的虚拟节点上环,3000个虚拟点均匀的分布在环上,可能a1-> b17-> b19->c200,那么还是拿个尺子,往环上一比,那么尺子压中的点,几乎有1/3是m1的,有1/3是m2的,有1/3是m3的,所以说整个环上拿着尺子比了一遍,节点几乎是1/3是m1的,有1/3是m2的,有1/3是m3的,实现了均匀分布。然后,加入一台机器m4,给m4分配1000个字符串(d1.....d1000),m4的1000个虚拟节点,帮m4上环,假设d1位置在c200与b98之间,通过顺时针找节点,d1需要向c200要数据,通过c200定位m3机器,将c200(m3)节点数据小与等于d1的数据物理的迁移至d1(m4)上,由于m4的虚拟节点数量也是1000,那么m4的虚拟节点会几乎均等向m1,m2,m3所控制的虚拟节点要数据,每个机器要1/12数据,要来三份就是3/12->1/4,这样又实现了均分。
4)虚拟节点技术打开之后,就更好玩了,比如m1机器性能特别强,m2、m3机器性能很平庸,m4机器性能最垃圾,那么给m1分配2000个虚拟节点,m2、m3分配1000个虚拟节点,m4分配500个虚拟节点,所以虚拟节点技术既能实现负载均衡,也能实现负载管理,无非就是调整虚拟节点的占有比例
一致性哈希可以说是分布式存储的基础,任何产品只要使用了一致性哈希,上述的这样的逻辑都会来一遍
总结:哈希函数上的设计是不是很酷,特别崇拜当初设计的那个人