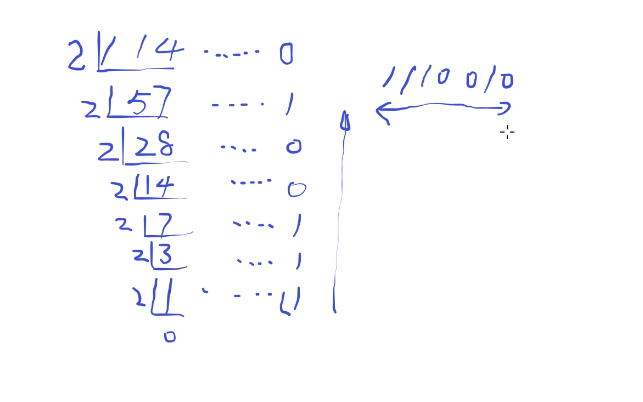ShiYu

# 二进制的整数

# 概念

  • 人为什么用十进制

    人有10个手指

  • 计算机为什么用二进制

    计算机最核心的计算单元是CPU

    CPU外面有许多引脚(通电使用)接收的高电频(1)与低电频(0)

    逢二进一

    image-20201207192311458

  • 10进制和2进制表数的共通点(基数) Radix

    基数(Radix)：基数排序

    ​ 16进制的基数 => 16

    ​ 10进制的基数 => 10

    ​ 8进制的基数 => 8

    ​ 2进制的基数 => 2

# 转换

  • 二进制与十进制的转换
    • 任何进制转换为十进制的算法
      • 基数的(n-1)位次幂
      • (二进制)01101011=> 20 x 1+21 x 1+23 x 1+25 x 1+26 x 1 => 107
      • (十六进制)0xAF => F x 160 + A x 161 => 175
      • (八进制) 047 => 7 x 80 + 4 x 81 => 39
      • 210以内记住
        • 20 => 1
        • 21 => 2
        • 22 => 4
        • 23 => 8
        • 24 => 16
        • 25 => 32
        • 26 => 64
        • 27 => 128
        • 28 => 256
        • 29 => 512
        • 210 => 1,024
        • 211 => 2,048
        • 212 => 4,096
        • 213 => 8,192
        • 214 => 16,384
        • 215 => 32,768
        • 216 => 65,536
    • 十进制转换二进制
      • 114 => 64 + 32 + 16 + 2 => 01110010
      • 153 => 128 + 16 + 8 + 1 => 10011001
      • 除2求余
      • image-20201207203120469

# 原码/反码/补码 *

  • 二进制0与二进制负数
    • 最高位变成符号位
    • 正数用原码表示，负数用补码表示
    • 正数的补码就是原码，补码主要用在负数上
    • 7 = 00000111(原码) => 反码是原码按位取反(11111000) => 补码是原码按位取反再加1(11111001)
    • 负数用补码表示，10进制负数转二进制，先求解对应正数，然后符号位定为1，其余位取反+1
      • -17转二进制 = 00010001(正数) => 10010001(符号位定为1) => 11101111(其余位取反+1)
    • 二进制负数转十进制，符号位不变，其余位取反+1，得到原码
      • 11000100转十进制 = 10111011(符号位不变，其余位取反) => 00111100(+1 得到原码) => -60
    • 为什么负数用补码表示？
      • 减法可以当做加法来运算
        • 只有加法器没有减法器
        • 5-3 => 5+(-3)
        • 5 => 0000,0101
        • -3 => 0000,0011(正数原码) => 1111,1100(其余位取反) => 1111,1101 (+1)
        • 0000,0101 + 1111,1101 => 0000,0010 => 2
      • 0的表述实现统一
        • 0的原码 8位 (0000,0000) => -0 (1000,0000) =>取反(1111,1111) => +1 9位(1,0000,0000) 溢出去掉第九位 还是=> 8位 (0000,0000)
        • 0的补码还是原码

# 二进制逻辑运算/位运算 **

  • & 按位与 遇0则0
    • 1 & 1 = 1
    • 1 & 0 = 0
    • 0 & 1 = 0
    • 0 & 0 = 0
  • | 按位或 遇1则1
    • 1 | 1 = 1
    • 1 | 0 = 1
    • 0 | 1 = 1
    • 0 | 0 = 0
  • ~ 按位取反 1-0 0-1
  • ^ 按位异或 不进位加 (相同为0，相异为1)
    • 1 ^ 1 = 0
    • 1 ^ 0 = 1
    • 0 ^ 1 = 1
    • 0 ^ 0 = 0
  • >> 逻辑右移 补符号位
    • 0100,1000 >> 1 => 右移一位 => 0010,0100 => 最高位补符号位 是0补0 是1补1
  • << 左移 补0
    • 0100,1001 << 1 => 左移一位 => 1001,0010 => 最低位永远补0
    • 移位运算与乘除运算的关系
    • 对于正整数往右移(>>)一位 => 相当于除以2
    • 8 => 0000,1000 >> 1 => 0000,0100(4) => 8/2 => 4
    • 往左移(<<)一位 => 相当于乘以2
  • >>>算术右移或无符号右移 高位永远补0
  • 关于位运算的简单面试题
    • 表示23最有效率的程序 => 1 <<3 => 2 << 2
    • a=3 b=4 最有效率的将a,b变量值置换
      • a = a ^ b => a(后) = a(原) ^ b
      • b = a ^ b => b = a(原) ^ b ^ b ==>> a(原)
      • a = a ^ b => a = a(原) ^ b ^ a(原) ==>> b

# 长整数与短整数的转换

  • 短整数 => 长整数 转换
    • 补符号位即可
      • (正数)0110,1101 => 0000,0000, 0110,1101
      • (负数)1100,0110 => 1111,1111,1100,0110
  • 长整数 => 短整数 转换
    • 精度丢失
      • 0000,0000 0000,0000 0000,0001 0110,1101
      • 上面从32位转换位8位 精度丢失 0110,1101

# 常用的单位概念

  • bit 一位
  • Byte 字节 => 8位
  • KB 1024Byte Kb 1024bit
  • MB 1024KB
  • GB 1024MB
  • TB 1024GB
  • .......

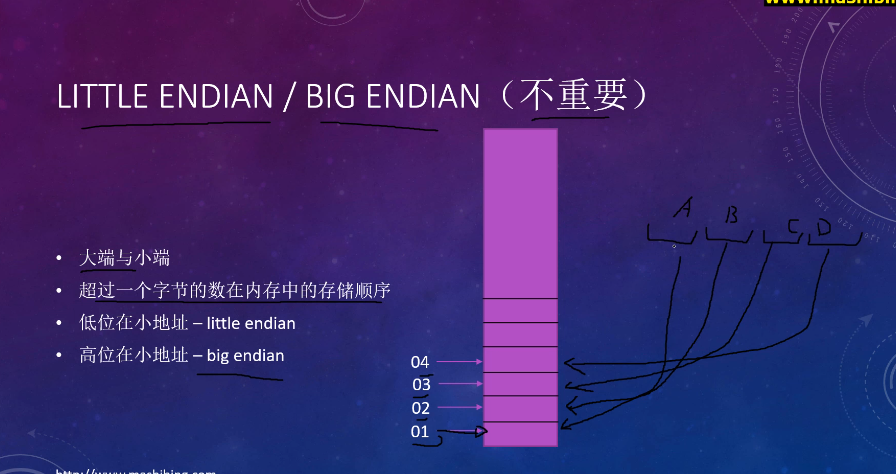
# BIG/LITTLE EBDIAN 内存中存储顺序

image-20201208010658820

image-20201208010827690

# 复习

image-20201208010943087

10进制转8进制 除8求余

10进制转16进制 除16求余

2进制转16进制 4位变成一个单位 2进制的8位 代表 16进制的2位 因为 28 = 162

# 二进制的小数

IEEE 754 浮点数表示

← 面向对象 →